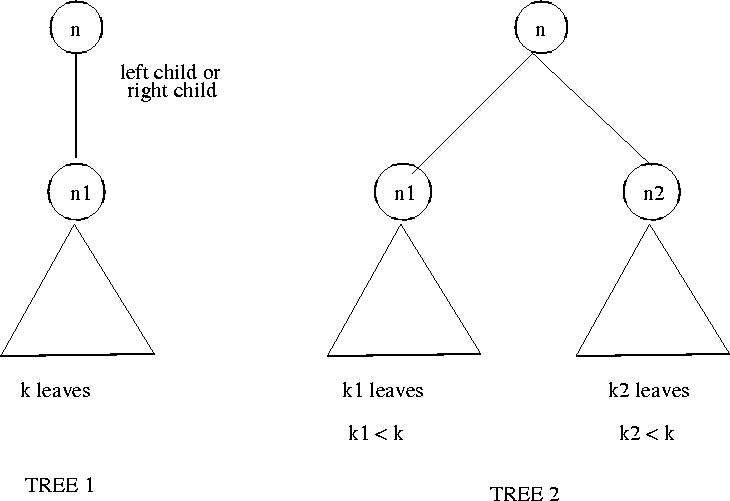
 |
We shall show the result for any binary tree with K leaves.
Suppose the result is not true. Suppose T is the counterexample with the fewest nodes.
T cannot be a single node because log 1 = 0. Let T
have k leaves.
T can only be of the following
two forms. Now see Figure 9.6.
 |
Suppose T is of the from Tree 1. The tree rooted at n1, has fewer nodes than T but the same number of leaves and the hence an even smaller counterexample than T. Thus T cannot be of Tree 1 form.
Suppose T is of the form of Trees 2. The trees T1 and T2 rooted at n1 and n2 are smaller than T and therefore the
| Average depth of T1 | logk1 | ||
| Average depth of T2 | logk2 |
Thus the average depth of T
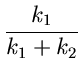 logk1
+ logk1
+ 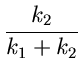 logk2
+ 1 logk2
+ 1 |
|||
| = | |||
| = | |||
logk |
This contradicts the premise that the average depth of T is < log k.
Thus T cannot be of the form of Tree 2.
Thus in any decision tree with n! leaves, the average path length to a leaf is at least