


Next:9.8.2
Result 2: Lower Bound on Average Case ComplexityUp:9.8
Lower Bound on Complexity for Sorting MethodsPrevious:9.8
Lower Bound on Complexity for Sorting Methods
9.8.1 Result 1: Lower Bound
on Worst Case Complexity
-
Given a list of n distinct elements, there are n! possible
outcomes that represent correct sorted orders.
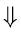
-
any decision tree describing a correct sorting algorithm on a list of n
elements will have at least n! leaves.
-
In fact, if we delete nodes corresponding to unnecessary comparisons and
if we delete leaves that correspond to an inconsistent sequence of comparison
results, there will be exactly n! leaves.
The length of a path from the root to a leaf gives the number of comparisons
made when the ordering represented by that leaf is the sorted order for
a given input list L.
-
The worst case complexity of an algorithm is given by the length of the
longest path in the associated decision tree.
-
To obtain a lower bound on the worst case complexity of sorting algorithm,
we have to consider all possible decision trees having n! leaves
and take the minimum longest path.
In any decision tree, it is clear that the longest path will have a length
of at least log n!
Since
More Precisely,
| n! |
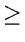 |
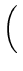 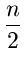 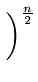 |
|
| |
|
|
|
| or log(n!) |
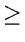 |
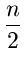 log log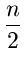 |
|
| |
|
|
|
| |
= |
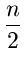 logn
- logn
- 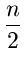 |
|
Thus any sorting algorithm that only uses comparisons has a worst case
complexity
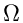 (nlog
n)
(nlog
n)



Next:9.8.2
Result 2: Lower Bound on Average Case ComplexityUp:9.8
Lower Bound on Complexity for Sorting MethodsPrevious:9.8
Lower Bound on Complexity for Sorting Methods
eEL,CSA_Dept,IISc,Bangalore
![]()