9.8 Lower Bound on Complexity for Sorting Methods

Result 1

The worst case complexity of any sorting algorithm that only uses key comparisons is 

                                                                                                                $$\Omega$$(nlog n)
 

Result 2

The average case complexity of any sorting algorithm that only uses key comparisons is 

                                                                                                               $$\Omega$$(nlog n)
 

The above results are proved using a Decision Tree which is a binary tree in which the nodes represent the status of the algorithm after making some comparisons.

Consider a node x in a decision tree and let y be its left child and zits right child. See Figure 9.4.
 
 

Figure 9.4: A decision tree scenario

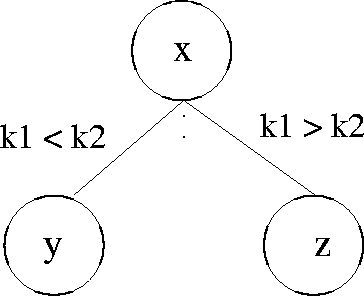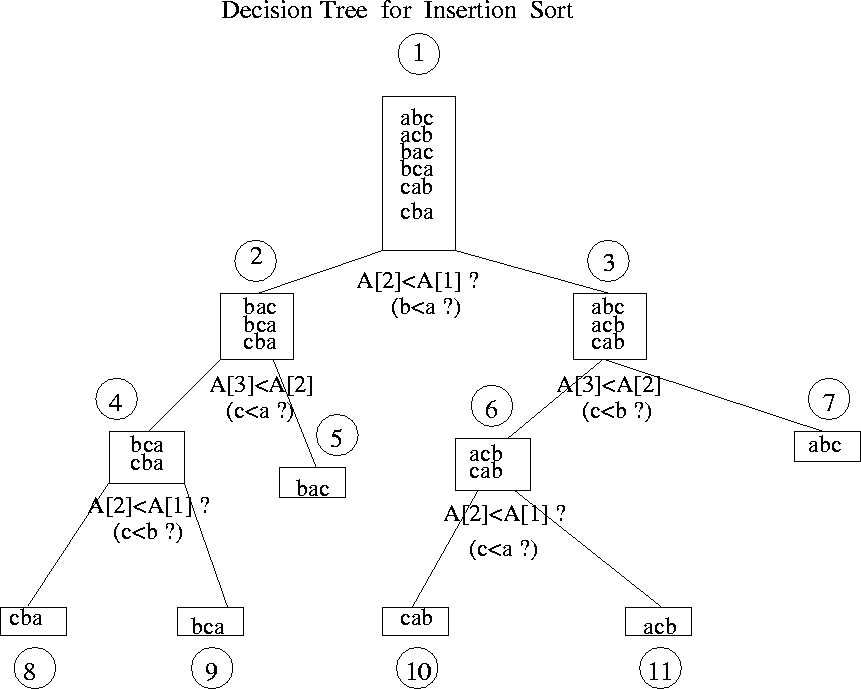
Basically, y represents a state consisting of the information known at x plus the fact that the key k₁ is less than key k₂. For a decision tree for insertion sort on 3 elements, see Figure 9.5.
 
 

Figure 9.5: Decision tree for a 3-element insertion sort