Sort each group of 5 elements by any algorithm and take the middle element from each group. This yields
![]() n/5
n/5![]() medians.
medians.
Blum, Floyd, Pratt, Rivest, Tarzan.
Sort each group of 5 elements by any algorithm and take the middle element from each group. This yields
![]() n/5
n/5![]() medians.
medians.
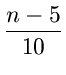
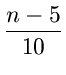
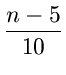
n![]() 75
75 ![]() 3
3![]()
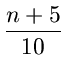
![]()
![]()
![]()
This would mean that, if n![]() 75, the pivot is greater than at least
75, the pivot is greater than at least ![]() elements and less than at least
elements and less than at least ![]() elements. Consequently, when we partition an array with this pivot, the kth
element is isolated to within a range of at most
elements. Consequently, when we partition an array with this pivot, the kth
element is isolated to within a range of at most ![]() of the elements.
of the elements.
keytype select (int i, j, k);
/* returns key of the kth largest element among A[i] ... A[j]*/
{
if((j - i) < 75)
find the kth largest by some simple algorithm
else {
for(m = 0;m![]() (j - i - 4)/5;m + +)
(j - i - 4)/5;m + +)
{
find the third element among A[i + 5 * m] ... A[i + 5 * m + 4]
and swap it with A[i + m];
pivot = select (i,(j - i - 4)/5,(j - i - 4)/10)
m = partition (i, j, pivot);
if(k![]() m
- i)
m
- i)
return (select (i, m - 1, k))
else
return (select (m, j,(k - (m - i)))
}
}
}
The worst case complexity of the above algorithm can be described by
| T(n) | C1 if n |
||
| C2n + T |
Let us guess the solution T(n) = Cn for
n > 75. For n![]() 75, assumeT(m)
75, assumeT(m) ![]() Cm
for m < n. Then
Cm
for m < n. Then
| T(n) | C2n + 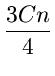 |
||
| C2n + |
Thus T(n) is O(n).