8.3.2 Prim's Algorithm

Next:8.3.3 Kruskal's AlgorithmUp:8.3 Minimum-Cost Spanning TreesPrevious:8.3.1 MST Property

8.3.2 Prim's Algorithm

This algorithm is directly based on the MST property. Assume that V = {1, 2,..., n}.

REF.: R.C. Prim. Shortest connection networks and some generalizations. Bell System Technical Journal, Volume 36, pp. 1389-1401, 1957.

{

T = $\phi$ ;

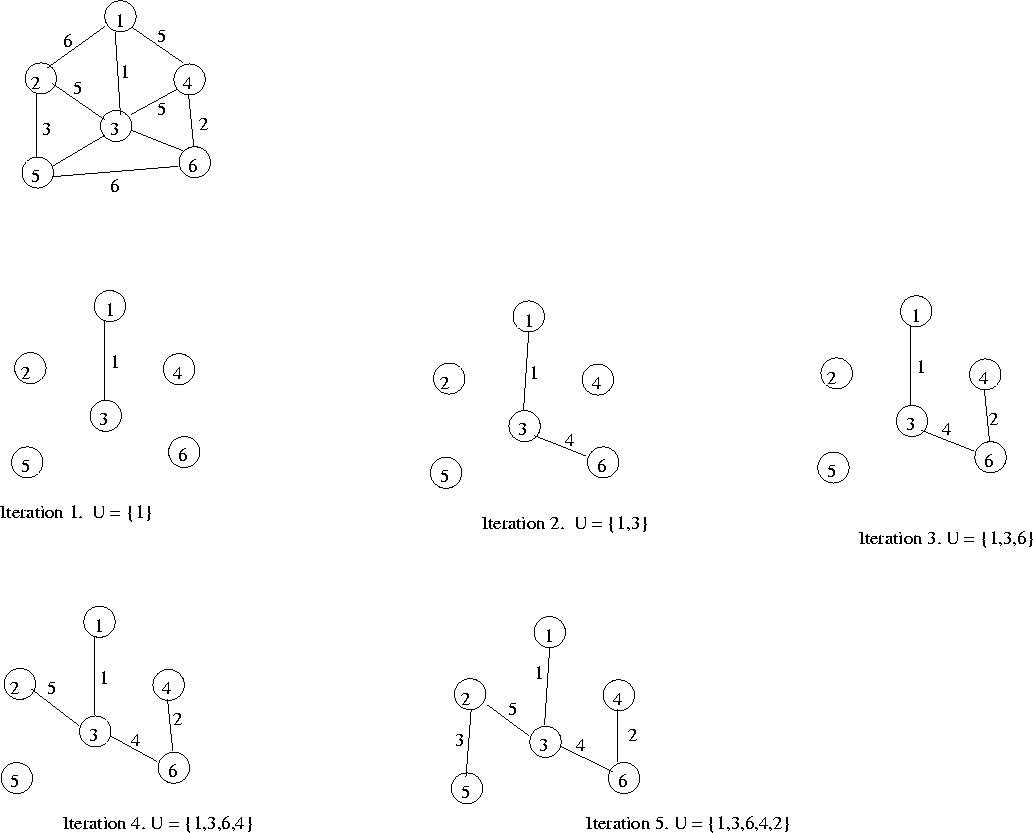
U = { 1 };

while (U $\neq$ V)

{

let (u, v) be the lowest cost edge

such that u $\in$ U and v $\in$ V - U;

T = T $\cup$ {(u, v)}

U = U $\cup$ {v}

}

See Figure 8.11 for an example.
O(n²) algorithm.

Proof of Correctness of Prim's Algorithm

Theorem: Prim's algorithm finds a minimum spanning tree.

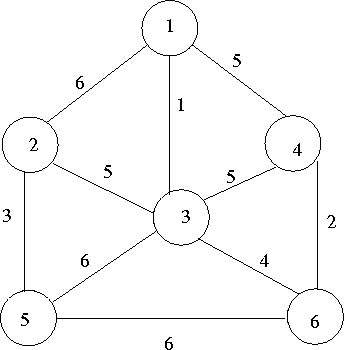
Proof: Let G = (V,E) be a weighted, connected graph. Let T be the edge set that is grown in Prim's algorithm. The proof is by mathematical induction on the number of edges in T and using the MST Lemma.

Basis: The empty set $\phi$ is promising since a connected, weighted graph always has at least one MST.

Induction Step: Assume that T is promising just before the algorithm adds a new edge e = (u,v). Let U be the set of nodes grown in Prim's algorithm. Then all three conditions in the MST Lemma are satisfied and therefore T U e is also promising.

When the algorithm stops, U includes all vertices of the graph and hence T is a spanning tree. Since T is also promising, it will be a MST.

Implementation of Prim's Algorithm

Use two arrays, closest and lowcost.

For i $\in$ V - U, closest[i] gives the vertex in U that is closest to i
For i $\in$ V - U, lowcost[i] gives the cost of the edge (i, closest(i))

**Figure 8.11:** Illustration of Prim's algorithm
$\begin{figure}\centerline{\psfig{figure=figures/Fprim1.ps,width=6.0in}}\end{figure}$

**Figure 8.12:** An example graph for illustrating Prim's algorithm
$\begin{figure}\centerline{\psfig{figure=figures/Fprim2.ps,width=2in}}\end{figure}$

At each step, we can scan lowcost to find the vertex in V - U that is closest to U. Then we update lowcost and closest taking into account the new addition to U.
Complexity: O(n²)

Example: Consider the digraph shown in Figure 8.12.

$\fbox{Step 1}$

U = {1}		V - U = {2, 3, 4, 5, 6}
closest		lowcost
V - U	U
2	1	6
3	1	1
4	1	5
5	1	$\infty$
6	1	$\infty$

Select vertex 3 to include in U

$\fbox{Step 2}$

U = {1, 3} V - U = {2, 4, 5, 6}

closest lowcost

V - U U

2 3 5

4 1 5

5 3 6

6 3 4

Now select vertex 6

$\fbox{Step3}$

U = {1, 3, 6} V - U = {2, 4, 5, 6}

closest lowcost

V - U U

2 3 5

4 6 2

5 3 6

Now select vertex 4, and so on

Next:8.3.3 Kruskal's AlgorithmUp:8.3 Minimum-Cost Spanning TreesPrevious:8.3.1 MST Property

eEL,CSA_Dept,IISc,Bangalore

$\fbox{Step 2}$

U = {1, 3}		V - U = {2, 4, 5, 6}
closest		lowcost

V - U	U
2	3	5
4	1	5
5	3	6
6	3	4
Now select vertex 6

$\fbox{Step3}$
U = {1, 3, 6}		V - U = {2, 4, 5, 6}
closest		lowcost

V - U	U
2	3	5
4	6	2
5	3	6
Now select vertex 4, and so on