


Next:8.4
Traveling Salesman ProblemUp:8.3
Minimum-Cost Spanning TreesPrevious:8.3.2
Prim's Algorithm
8.3.3 Kruskal's Algorithm
-
REF.
-
J.B. Kruskal. On the shortest spanning subtree of a graph and the traveling
salesman problem.
Proceedings of the American Mathematical Society,
Volume 7, pp. 48-50, 1956.
-
Complexity is O(elog e)
where e is the number of edges. Can be made even more efficient
by a proper choice of data structures.
-
Greedy algorithm
-
Algorithm:
Let G = (V, E)
be the given graph, with | V| = n
{
Start
with a graph T = (V, )
consisting of only the
)
consisting of only the
vertices
of G and no edges; /* This can be viewed as n
connected
components, each vertex being one connected component
*/
Arrange E in the order of increasing
costs;
for (i
= 1, i n
- 1, i + +)
n
- 1, i + +)
{ Select the next smallest
cost edge;
if (the edge connects
two different connected components)
add the edge to T;
}
}
-
At the end of the algorithm, we will be left with a single component that
comprises all the vertices and this component will be an MST for G.
Proof
of Correctness of Kruskal's Algorithm
Theorem: Kruskal's algorithm finds a minimum spanning tree.
Proof: Let G = (V, E) be a weighted, connected graph. Let T be
the edge set that is grown in Kruskal's algorithm. The proof is by mathematical
induction on the number of edges in T.
-
We show that if T is promising at any stage of the algorithm, then it is
still promising when a new edge is added to it in Kruskal's algorithm
-
When the algorithm terminates, it will happen that T gives a solution to
the problem and hence an MST.
Basis: T =  is promising since a weighted connected graph always has at least one MST.
is promising since a weighted connected graph always has at least one MST.
Induction Step: Let T be promising just before adding a new edge
e
= (u, v). The edges T divide the nodes of G into one or more
connected components. u and v will be in two different components. Let
U be the set of nodes in the component that includes u. Note that
-
U is a strict subset of V
-
T is a promising set of edges such that no edge in T leaves U (since an
edge T either has both ends in U or has neither end in U)
-
e is a least cost edge that leaves U (since Kruskal's algorithm, being
greedy, would have chosen e only after examining edges shorter than e)
The above three conditions are precisely like in the MST Lemma and hence
we can conclude that the T {e} is also promising. When the algorithm stops, T gives not merely
a spanning tree but a minimal spanning tree since it is promising.
{e} is also promising. When the algorithm stops, T gives not merely
a spanning tree but a minimal spanning tree since it is promising.
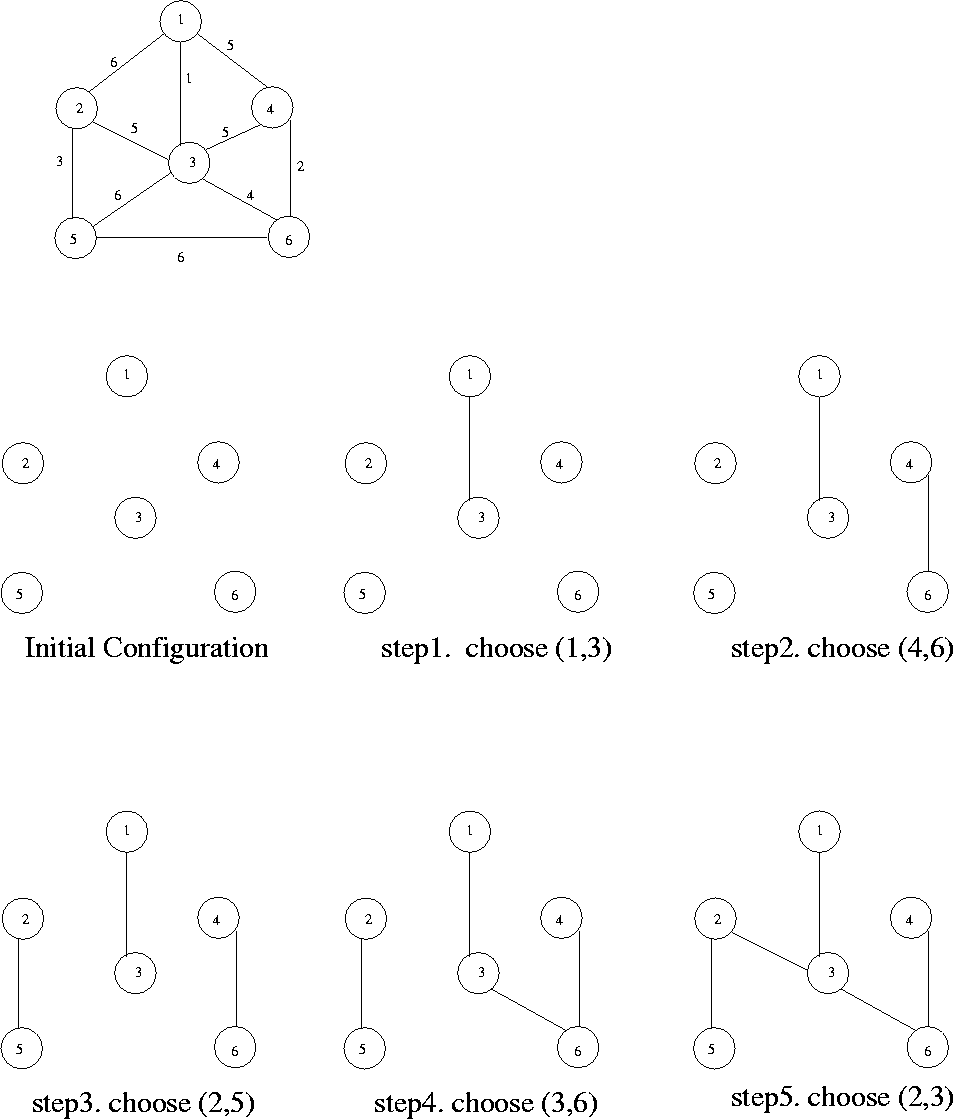
Figure 8.13: An illustration of Kruskal's algorithm
 |
-
Program
void kruskal (vertex-set V; edge-set
E; edge-set T)
int ncomp; /* current number of components
*/
priority-queue edges /* partially ordered tree */
mfset components; /* merge-find set data structure
*/
vertex u, v; edge
e;
int nextcomp; /* name for new component */
int ucomp, vcomp; /* component names */
{
makenull
(T); makenull (edges);
nextcomp = 0; ncomp = n;
for (v V)
/* initialize a component to have one vertex of
V*/
V)
/* initialize a component to have one vertex of
V*/
{
nextcomp++ ;
initial (nextcomp, v, components);
}
for (e E)
E)
insert (e, edges); /* initialize priority queue of edges
*/
while (ncomp > 1)
{
e = deletemin (edges);
let e = (u, v);
ucomp = find(u, components);
vcomp = find(v, components);
if (ucomp! = vcomp)
{
merge (ucomp, vcomp, components);
ncomp = ncomp - 1;
}
}
}
Implementation
-
Choose a partially ordered tree for representing the sorted set of edges
-
To represent connected components and interconnecting them, we need to
implement:
-
1.
-
MERGE (A, B, C) . . . merge components A and B in C and call the result
A or B arbitrarily.
-
2.
-
FIND (v, C) . . . returns the name of the component of C of which
vertex v is a member. This operation will be used to determine whether
the two vertices of an edge are in the same or in different components.
-
3.
-
INITIAL (A, v, C) . . . makes A the name of the component in C containing
only one vertex, namely v
-
The above data structure is called an MFSET
Running Time of Kruskal's Algorithm
-
Creation of the priority queue
-
*
-
If there are e edges, it is easy to see that it takes O(elog
e)
time to insert the edges into a partially ordered tree
-
*
-
O(e) algorithms are possible for this problem
-
Each deletemin operation takes O(log e) time in the worst
case. Thus finding and deleting least-cost edges, over the while iterations
contribute O(log e) in the worst case.
-
The total time for performing all the merge and find depends on the method
used.
| O(elog e) |
without path compression |
O(e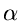 (e)) (e)) |
with the path compression, where |
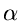 (e) (e) |
is the inverse of an Ackerman function. |
Example: See Figure 8.13.
E = {(1,3), (4,6), (2,5), (3,6), (3,4), (1,4), (2,3), (1,2), (3,5),
(5,6) }



Next:8.4
Traveling Salesman ProblemUp:8.3
Minimum-Cost Spanning TreesPrevious:8.3.2
Prim's Algorithm
eEL,CSA_Dept,IISc,Bangalore
![]() )
consisting of only the
)
consisting of only the
![]() n
- 1, i + +)
n
- 1, i + +)
