8.3 Minimum-Cost Spanning Trees

Let G = (V, E) be a connected graph in which each edge (u, v) $\in$E has an associated cost C(u, v).

• A Spanning Tree for G is a subgraph of G that it is a free tree connecting all vertices in V. The cost of a spanning tree is the sum of costs on its edges.
• An MST of G is a spanning tree of G having a minimum cost.
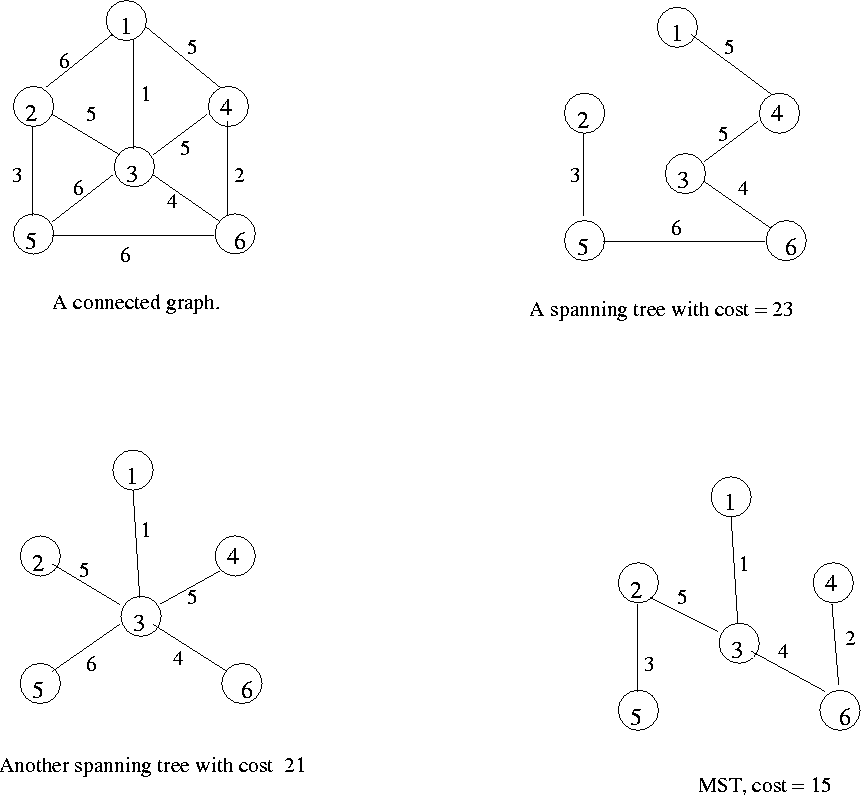
• See Figure 8.4 for several examples.

Figure 8.4: Spanning trees in a connected graph