8.3.1 MST Property

SupposeG = (V, E)is a connected graph with costs defined on all e$\in$E. Let U be some proper subset of V.

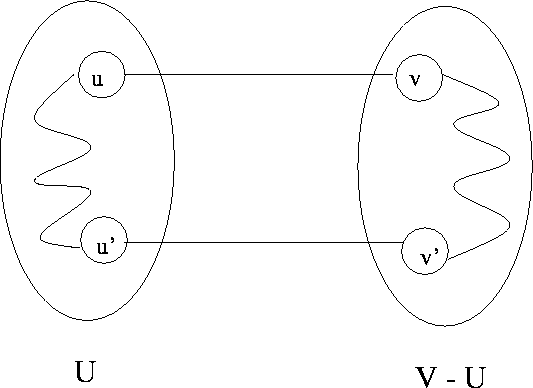
If (u, v) is an edge of lowest cost such that u$\in$Uand v$\in$V - U, then there exists an MST that includes (u, v) as an edge. See Figure 8.5.
 

Figure 8.5: An illustration of MST property

Proof of MST Property

Suppose to the contrary that there is no MST for the graph Gwhich includes the edge (u, v).

Let T be any MST of G. By our assumption, T does not contain (u, v). Adding (u, v) to Twill introduce a cycle since T is a free tree. This cycle involves (u, v). Therefore there is a path fromv to u that does not pass through this edge. This means that$\exists$another edge (u', v') in T such that u'$\in$Uandv'$\in$V - U. See Figure 8.6.
 

Figure 8.6: Construction of a minimal spanning tree

Deleting edge (u', v') breaks the cycle and yields a spanning tree T' whose cost is certainly $\leq$ that of T since C(u, v) $\leq$C(u', v'). Thus we have constructed an MST that includes (u, v).
 

Figure 8.7: An example graph for finding an MST

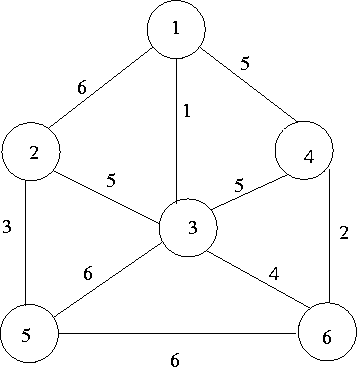To illustrate, consider the graph in Figure 8.7 and refer to Figures 8.8 and 8.9. Consider the sets:

U = {1, 2, 5}

V - U = {3, 4, 6}.

Figure 8.8: A spanning tree in the above graph, with cost 26

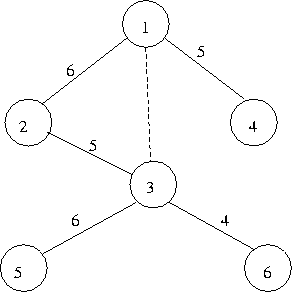Spanning tree with cost = 26. Now, least cost edge from U to V - U is (1,3).

By including (1,3) in the above spanning tree, a cycle will form (for example, 1-2-3-1). Let us replace the edge (2,3) by the edge (1,3).
 

Figure 8.9: Another spanning tree, but with cost 22

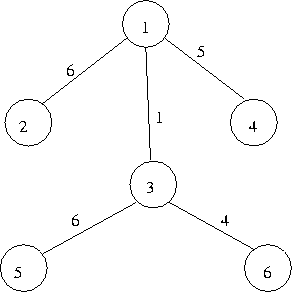This has yielded a ST with cost = 22

DEF.

A set of edges T in a connected graph promising if it can be extended to produce a minimal spanning tree for the graph.

• By definition, T = $\phi$ is always promising since a weighted connected graph always has at least one MST.
• Also, if a promising set of edges T is a spanning tree, then it must be an MST.

Def: An edge is said to leave a given set of nodes if exactly one end of this edge is in the set.

MST Lemma: Let

• G = (V, E) be weighted connected graph
• U $\subset$V a strict subset of nodes in G
• T $\subseteq$E a promising set of edges in E such that no edge in T leaves U
• e a least cost edge that leaves U

Then the set of edgesT^' = T$\cup$ {e} is promising.
 

Figure 8.10: Illustration of MST Lemma

Proof

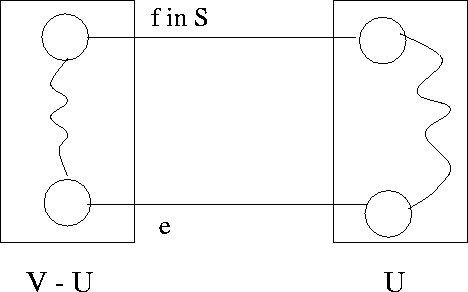
Since T is promising, it can be extended to obtain an MST, says S. If e$\in$ S, there is nothing to prove.

If e$\in$  S, then we add edge e to S, we create exactly one cycle (since S is a spanning tree). In this cycle, since e leaves U there exists at least one other edge, f say, that also leaves U (otherwise the cycle could not close). See Figure 8.10.

If we now remove f, the cycle disappears and we obtain a new tree R that spans G.

Note thatR = (S$\cup$ {e}) - {f}

Also note that weight of e$\leq$weight of f since e is a least cost edge leaving U.

Therefore R is also an MST and it includes edge e. Furthermore T$\subseteq$  R and so can be extended to the MST R. Thus T is a promising set of edges.