6.2 Binomial Queues

REF.

Jean Vuillemin. A data structure for manipulating priority queues. Communications of the ACM, Volume 21, Number 4, pp.309-315, 1978.

REF.

Mark R. Brown. Implementation and analysis of binomial queue algorithms. SIAM Journal on Computing, Volume 7, Number 3, pp. 298-319, 1978.

• Support merge, insert, and deletemin operations in O(log n) worstcase time.
• A binomial queue is a forest of heap-ordered trees.
  • Each of the heap-ordered trees is of a constrained form known as a binomial tree.

  

Figure 6.5: Examples of Binomial Trees

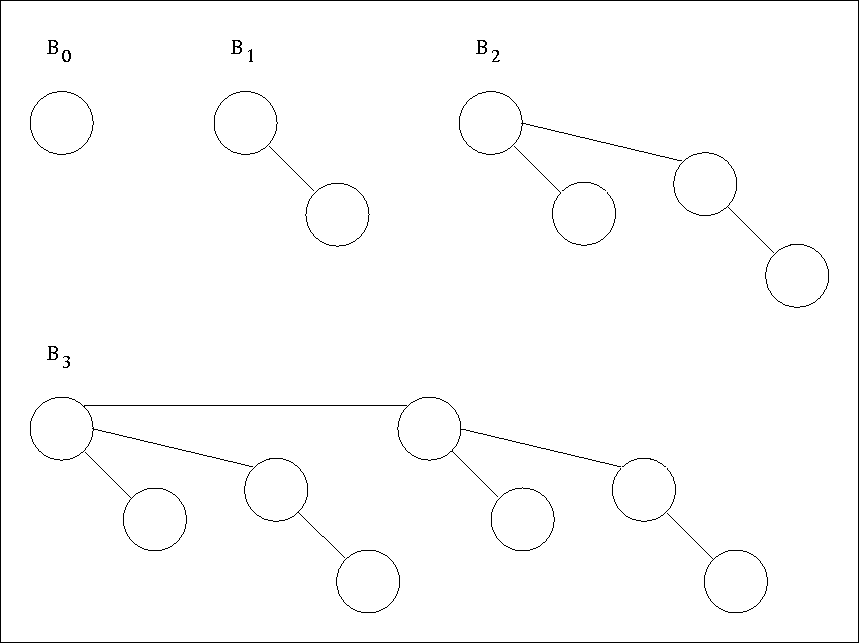• A binomial tree of height 0 is a one-node tree; A binomial tree B_k of height k is formed by attaching a binomial tree B_{k - 1} to the root of another binomial tree, B_{k - 1}.
• See Figure 6.5 for an example of binomial tree.
• A binomial tree B_k consists of a root with children B₀, B₁, ... B_{k - 1}.
• B_k has exactly 2^k nodes.
• Number of nodes at depth d is kC_d
• If we impose heap order on the binomial trees and allow at most one binomial tree of any height, we can uniquely represent a priority queue of any size by a forest of binomial trees.
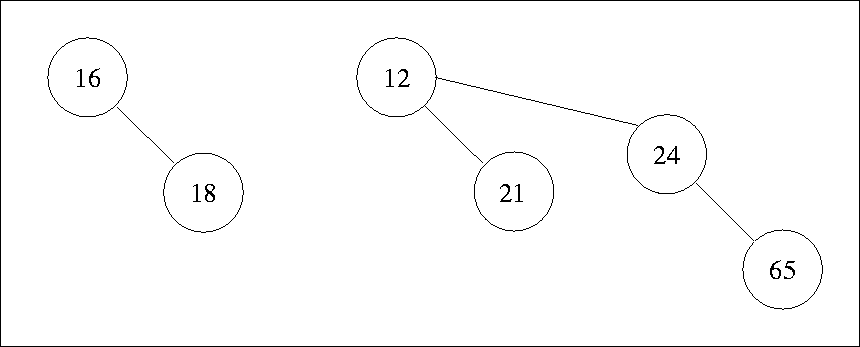
• Example: A priority queue of size 13 could be represented by the forest B₃, B₂, B₀. A natural way of writing this is: 1101. See Figure 6.6 for a binomial queue with six elements.

  

Figure 6.6: A binomial queue H₁ with six elements