6.2.3 Lazy Binomial Queues

Binomial queues in which merging is done lazily.

Here, to merge two binomial queues, we simply concatenate the two lists of binomial trees. In the resulting forest, there may be several trees of the same size.

Because of the lazy merge, merge and insert are both worstcase 0(1) time.

• Deletemin:
• Convert lazy binomial queue into a standard binomial queue
• Do deletemin as in standard queue.

Fibonacci Heaps

Fibonacci heap supports all basic heap operations in 0(1) amortized time, with the exception of deletemin and delete which take 0(log n) amortized time.

Fibonacci heaps generalize binomial queues by adding two new concepts:

• A different implementation of decrease-key
• Lazy merging: Two heaps are merged only when it is required.

It can be shown in a Fibonacci heap that any node of rank r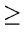$\geq$ 1 has at least Fr + 1 descendents.