Define the cost of each insertions to be
- 1time unit + an extra unit for each linking step
Thus the total will be n units plus the total number of linking steps. - The 1st, 3rd, ... and each odd-numbered step requires no linking steps since there is no B0 present.
- A quarter of the insertions require only one linking step: 2nd, 6th, 10, ...
- One eighth of insertions require two linking steps.
We could do all this and bound the number of linking steps by n.
The above analysis will not help when we try to analyze a sequence of operations that include more than just insertions.
Consider the result of an insertion.
- If there is no B0 tree, then the insertion costs one time unit. The result of insertion is that there is now a B0 tree and the forest has one more tree.
- If there is a B0 tree but not B1 tree, then insertion costs 2 time units. The new forest will have a B1 tree but not a B0 tree. Thus number of trees in the forest is unchanged.
- An insertion that costs 3 time units will create a B2 tree but destroy a B0 and B1, yielding one less tree in the forest.
- In general, an insertion that costs c units results in a net
increase of 2 - c trees. Since
- a Bc - 1 tree is created
- all Bi trees, 0
 i
i  c - 1 are removed.
c - 1 are removed.
Let ti = 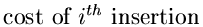
ci = 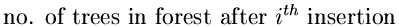
We have
c0 = 0 ti + (ci - ci - 1) = 2