6.1.2 Creating Heap

Given a set of n elements, the problem here is to create a heap of these elements.

• obvious approach is to insert the n elements, one at a time, into an initially empty heap. Since the worstcase complexity of inserts is O (log n), this approach has a worstcase running time of O ( n log n)
• Another approach, purposed by Floyd in 1964, is to use a procedure called ``pushdown'' repeatedly, starting with the array consisting of the given n elements in the input-order.
• The function pushdown (first,last) assumes that the elements a[first], ..., a[last] obey the heap property, except possibly the children of a[first]. The function pushes down a[first] until the heap property violation is stopped.
• The following code will accomplish what is required:


$\parbox{5in}{for $ (i = \frac{n}{2} ; \ i \geq 1; \ i --)$\space \\pushdown (i,n)}$

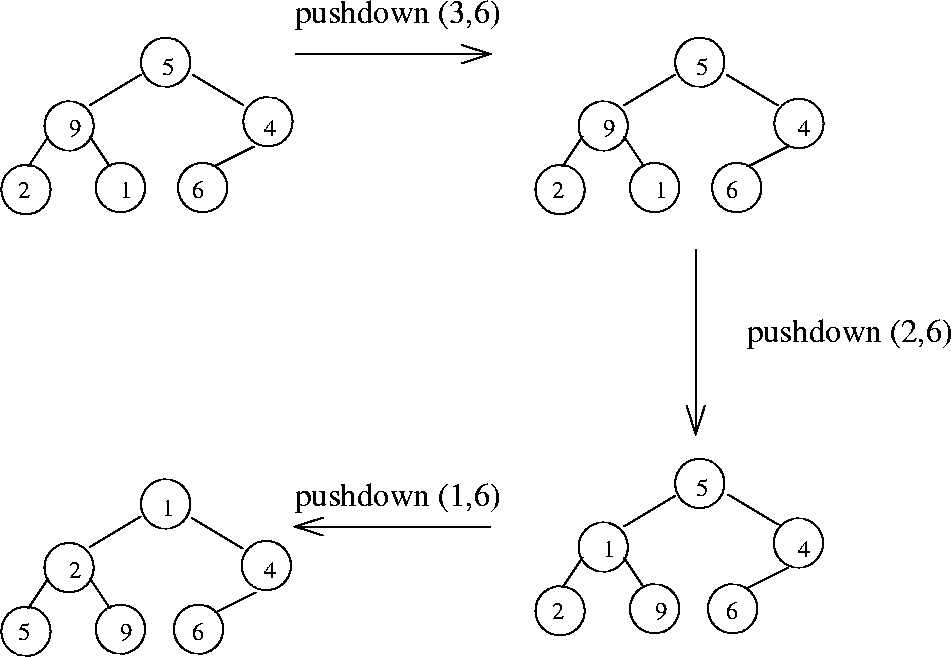
• Figure 6.4 shows an example of this for an array [5 9 4 2 1 6]
• The worstcase complexity of this approach can be shown to b O (n) by virtue of the following result.

Figure 6.4: Creation of heap

Result: For the perfect binary tree of height h containing2h + 1 - 1 nodes, the sum of the heights of the nodes is 2h + 1 - 1 - (h + 1).

Proof: The perfect or full binary tree of height h has 1 node at height h, 2 nodes art height (h-1), 4 nodes at height (h-2), ...

Therefore the required sum S is given by  

S	= 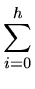$$\sum^{h}_{i=0}$$2i(h - i)
	= h + 2(h - 1) + 4(h - 2) + ... + 2h - 1

Multiplying both sides by 2 yields  

2S =	2h + 4(h - 1) + 8(h - 2) + ... + 2h

Subtracting this above equation from the equation prior to that, we obtain 
S = 2h + 1 - 1 - (h + 1)
 It is easy to see that the above is an upper bound on the sum of heights of nodes of a complete binary tree. Since a complete binary tree of height h has between 2h and 2h + 1 nodes, the above sum is therefore O (n) where n is the number of nodes in the heap.

Since the worstcase complexity of the heap building algorithm is of the order of the sum of heights of the nodes of the heap built, we then have the worst-case complexity of heap building as O (n).