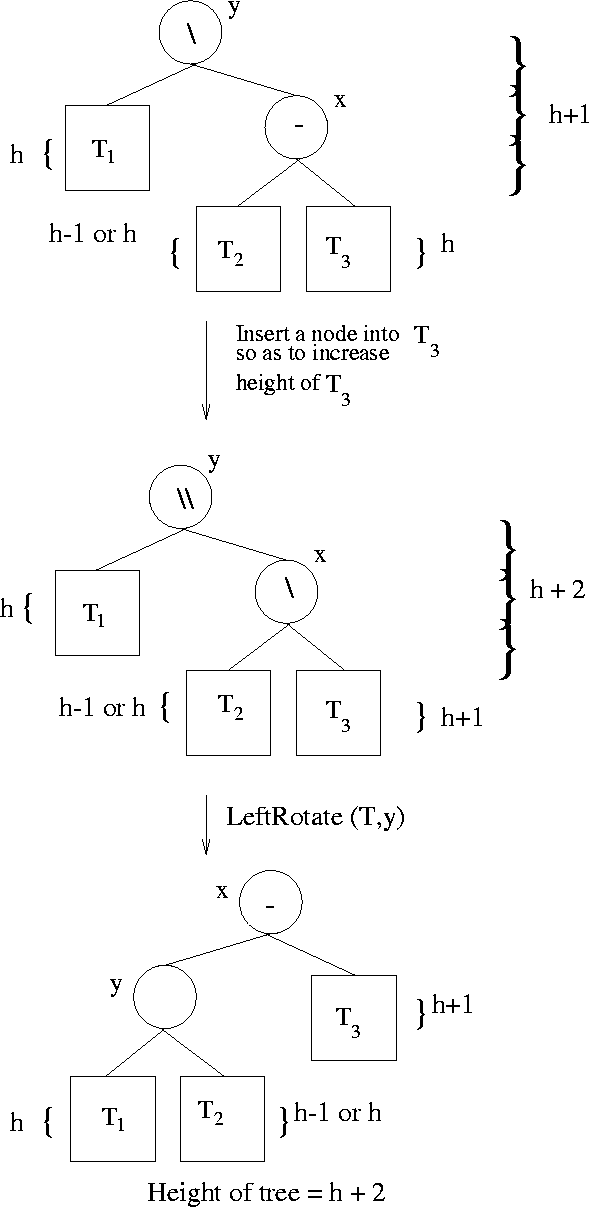5.1.2 AVL Trees: Insertions and Deletions

• While inserting a new node or deleting an existing node, the resulting tree may violate the (stringent) AVL property. To reinstate the AVL property, we use rotations. See Figure 5.4.

Rotation in a BST

• Left rotation and right rotation can be realized by a three-way rotation of pointers.

• Left Rotation:

  temp	=	p $\rightarrow$ right ;
  p $\rightarrow$ right	=	temp $\rightarrow$ left ;
  temp $\rightarrow$ left	=	p ;
  p	=	temp ;

• Left rotation and right rotation preserve

  *

  BST property

  *

  Inorder ordering of keys

  Problem Scenarios in AVL Tree Insertions

  • left subtree of node has degree higher by $\geq$ 2
    • left child of node is left high (A)
    • left child or node is right high (B)
  • right subtree has degree higher by $\geq$ 2
    • right child of node is left high (C)
    • right child or node is right high (D)

• The AVL tree property may be violated at any node, not necessarily the root. Fixing the AVL property involves doing a series of single or double rotations.

• Double rotation involves a left rotation followed or preceded by a right rotation.

• In an AVL tree of height h, no more than $\lceil$${\frac{h}{2}}$$\rceil$rotations are required to fix the AVL property.

  

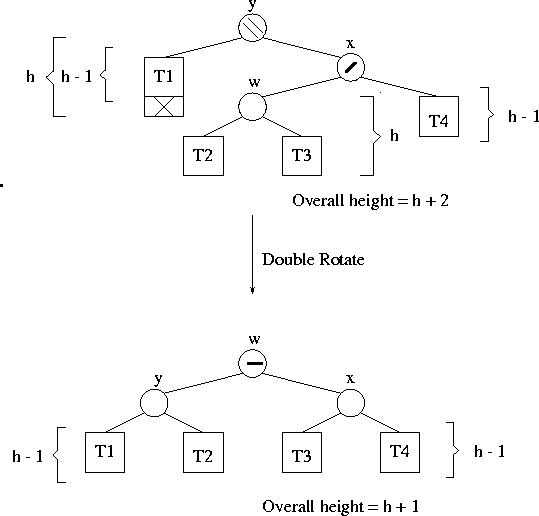
Figure 5.5: Insertion in AVL trees: Scenario D

  

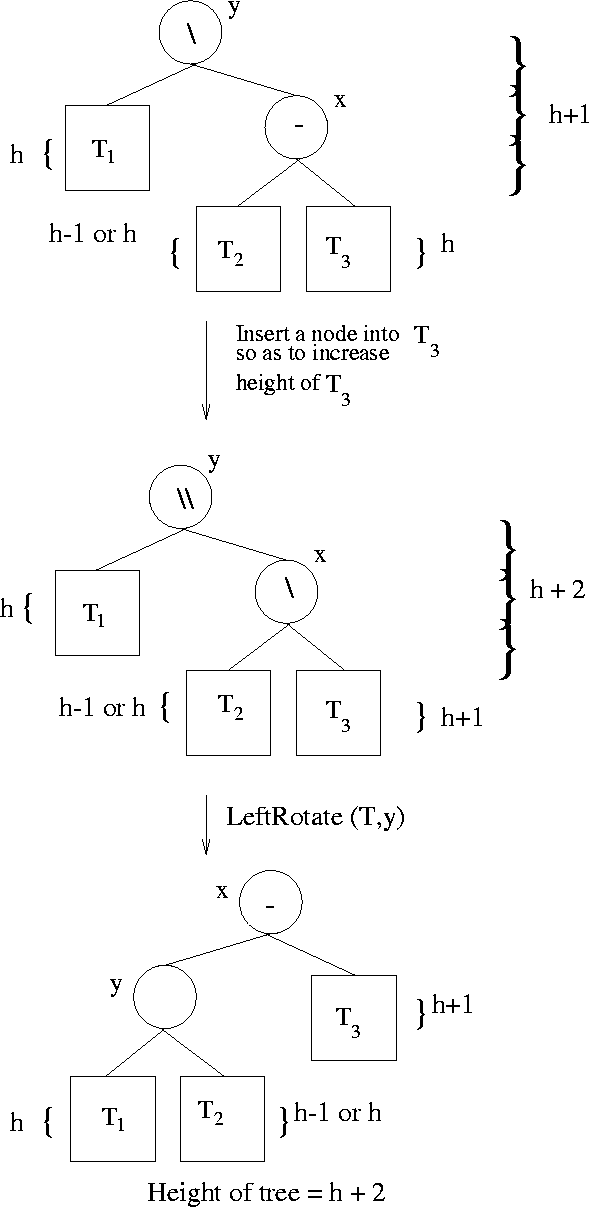Figure 5.6: Insertion in AVL trees: Scenario C

  

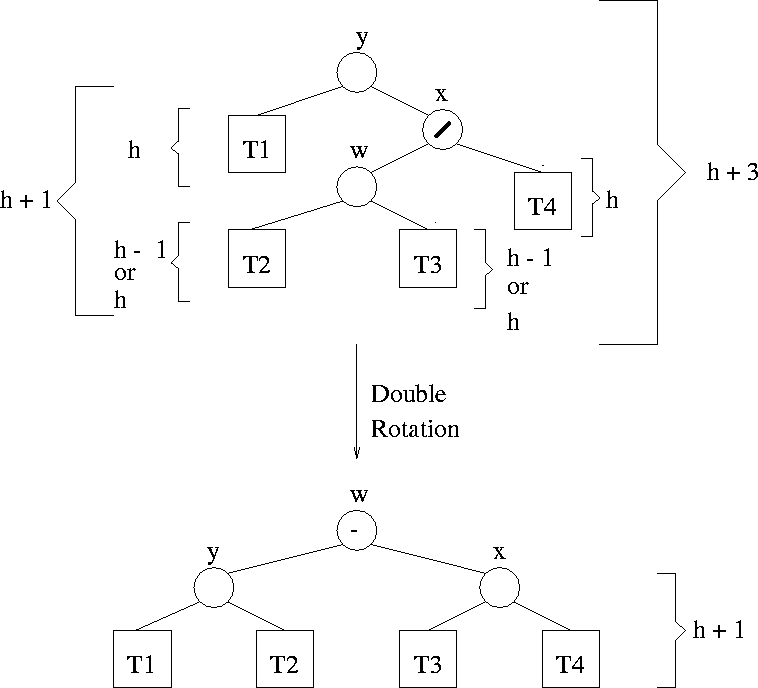Figure 5.7: Deletion in AVL trees: Scenario 1

  

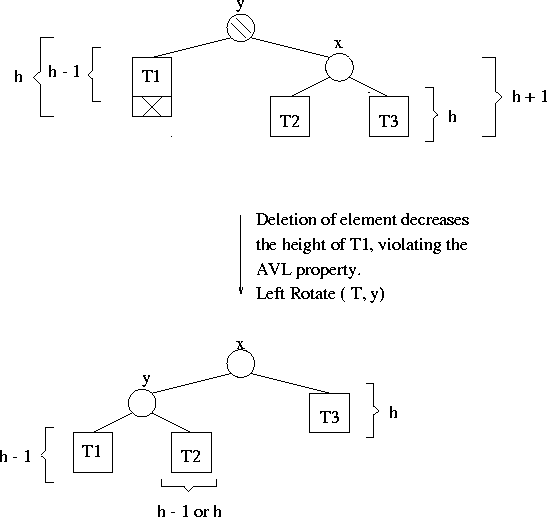Figure 5.8: Deletion in AVL trees: Scenario 2

Insertion: Problem Scenario 1: (Scenario D)

Scenario A is symmetrical to the above. See Figure 5.5.

Insertion: Problem Scenario 2: (Scenario C)

Scenario B is symmetrical to this. See Figure 5.6.

Deletion: Problem Scenario 1:

Depending on the original height of T₂, the height of the tree will be either unchanged (height of T₂ = h) or gets reduced (if height of T₂ = h - 1). See Figure 5.7.

There is a scenario symmetric to this.

Deletion: Problem Scenario 2:

See Figure 5.8. As usual, there is a symmetric scenario.