


Next: 5.2.1 Height of a Red-Black Tree
Up: 5. Balanced Trees
Previous: 5.1.2 AVL Trees: Insertions and Deletions
- Binary search trees where no path from the root to a leaf is more than
twice as long as any other path from the root to a leaf.
- REF.
- R. Bayer. Symmetric binary B-trees: Data Structures and maintenance
algorithms, Acta Informatica, Volume 1, pp.290-306, 1972.
Definition
A BST is called an RBT if it satisfies the following four properties.
- 1.
- Every node is either red or black
- 2.
- Every leaf is black (Missing node property)
- 3.
- If a node is red, then both its children are black
(RED constraint)
- 4.
- Every simple path from a node to a descendent leaf contains
the same number of black nodes
(BLACK constraint)
Black-Height of a Node
- Number of black nodes on any path from, but not including a node x to a
leaf is called the black height of x and is denoted by bh(x).
- Black height of an RBT is the black height of its root.
- Each node of a red black tree contains the following fields.
| colour |
key |
left |
right |
parent |
- If a child of a node does not exist, the corresponding pointer field will
be NULL and these are regarded as leaves.
- Only the internal nodes will have key values associated with them.
- The root may be red or black.
Examples : See Figures 5.9 and 5.10.
Figure 5.9:
A red-black tree with black height 2
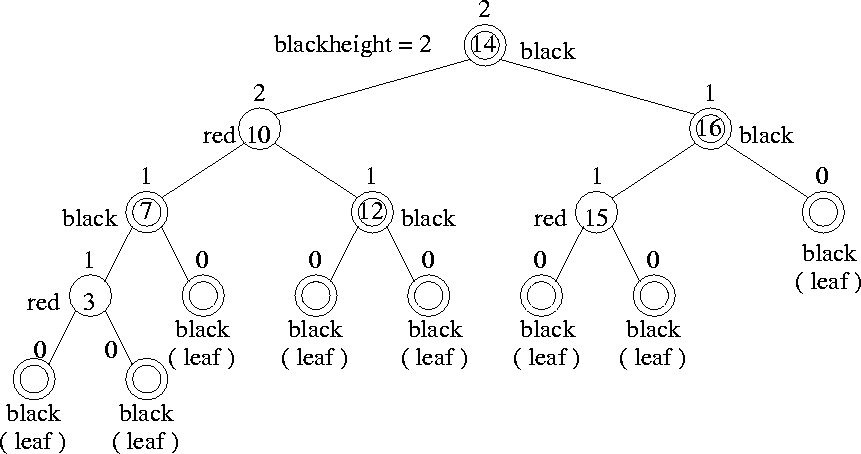 |
Figure 5.10:
Examples of red-black trees
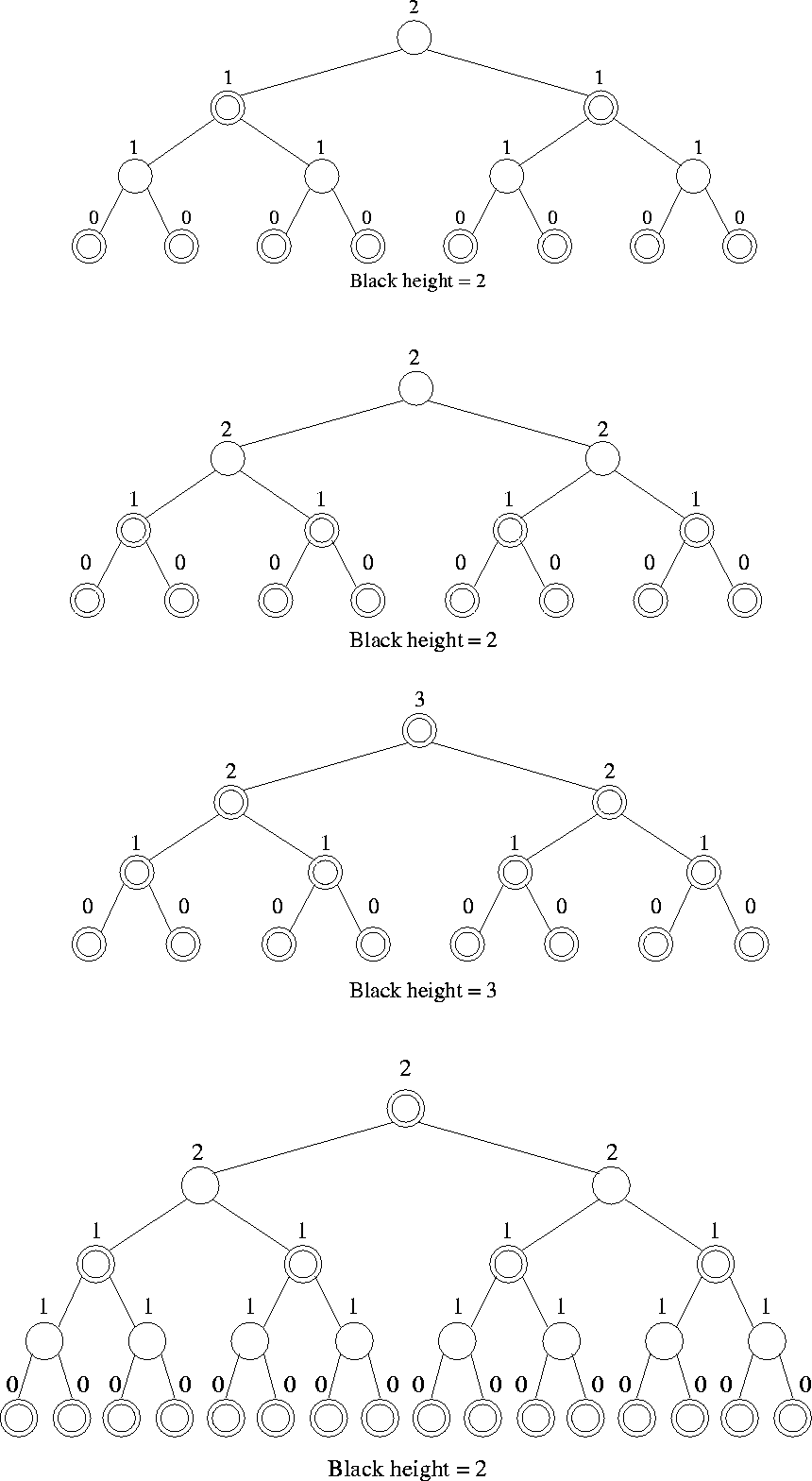 |



Next: 5.2.1 Height of a Red-Black Tree
Up: 5. Balanced Trees
Previous: 5.1.2 AVL Trees: Insertions and Deletions
eEL,CSA_Dept,IISc,Bangalore
