nextupprevious
Next:5.1.1 Maximum Height of an AVL TreeUp:5. Balanced TreesPrevious:5. Balanced Trees

5.1 AVL Trees

Also called as: Height Balanced Binary Search Trees.
REF.
G.M. Adel'son-Vel'skii and E.M. Landis. An algorithm for the organization of information. Soviet Mathematics Monthly Volume 3, pp.1259-1263, 1962.
Search, Insertion, and Deletion can be implemented in worst case O(log n) time

Definition

An AVL tree is a binary search tree in which

1.
the heights of the right subtree and left subtree of the root differ by at most 1
2.
the left subtree and the right subtree are themselves AVL trees
3.
A node is said to be
left-high if the left subtree has /
  greater height  
     
right-high if the right subtree has  
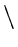  greater height $ \backslash$
     
equal if the heights of the LST and  
  RST are the same -
Figure 5.1: Examples of AVL trees
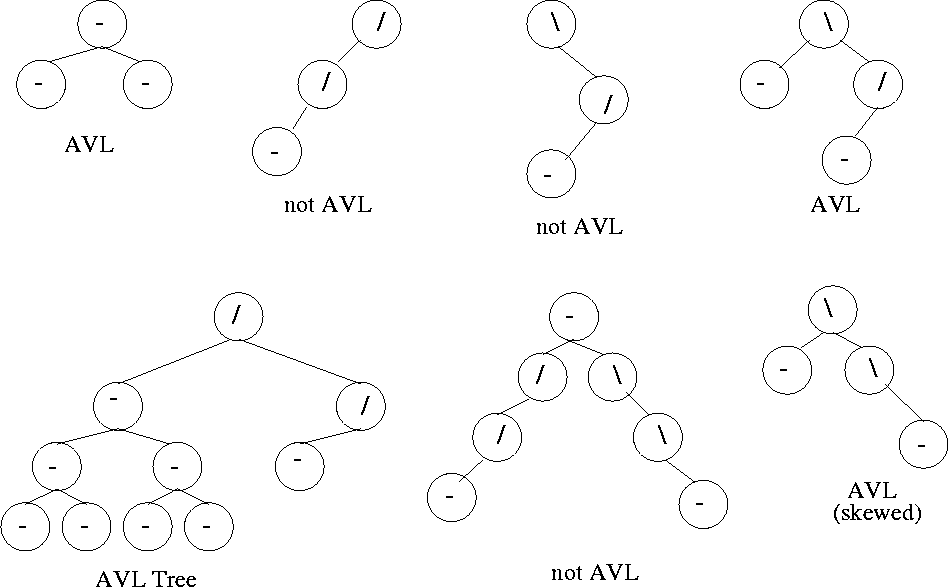\begin{figure}\centerline{\psfig{figure=figures/Favl1.ps,width=5.5in}}\end{figure}

Examples: Several examples of AVL trees are shown in Figure 5.1.
 
 

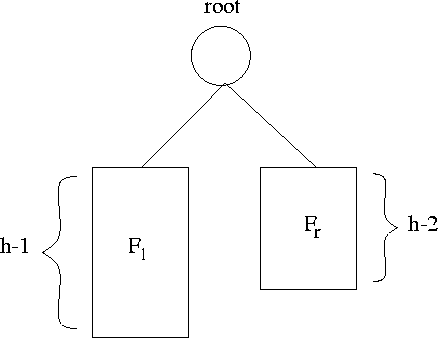
Figure 5.2: An AVL tree with height h
\begin{figure}\centerline{\psfig{figure=figures/Favl2.ps,height=5cm}}\end{figure}

 

nextupprevious
Next:5.1.1 Maximum Height of an AVL TreeUp:5. Balanced TreesPrevious:5. Balanced Trees
eEL,CSA_Dept,IISc,Bangalore