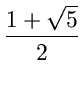Next:5.1.2
AVL Trees: Insertions and DeletionsUp:5.1
AVL TreesPrevious:5.1
AVL Trees
5.1.1 Maximum Height of an AVL
Tree
What is the maximum height of an AVL tree having exactly n nodes? To answer
this question, we will pose the following question:
What is the minimum number of nodes (sparsest possible AVL tree) an
AVL tree of height h can have ?
-
Let Fh be an AVL tree of height h, having the minimum
number of nodes. Fh can be visualized as in Figure 5.2.
-
Let Fl and Fr be AVL trees which are
the left subtree and right subtree, respectively, of Fh.
Then Fl or Fr must have height h-2.
-
Suppose Fl has height h-1 so that Fr
has height h-2. Note that Fr has to be an AVL tree having
the minimum number of nodes among all AVL trees with height of h-1. Similarly,
Fr will have the minimum number of nodes among all AVL
trees of height h--2. Thus we have
| Fh| = | Fh - 1| + | Fh
- 2| + 1
-
where | Fr| denotes the number of nodes in Fr.
Such trees are called Fibonacci trees. See Figure 5.3.
Some Fibonacci trees are shown in Figure 4.20. Note that | F0|
= 1 and | F1| = 2.
-
Adding 1 to both sides, we get
| Fh| + 1 = (| Fh - 1| + 1)
+ (| Fh - 2| + 1)
-
Thus the numbers | Fh| + 1 are Fibonacci numbers. Using
the approximate formula for Fibonacci numbers, we get
| Fh| + 1 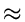
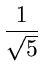
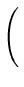
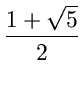

-
-
h
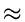 1.44log| Fn|
1.44log| Fn|
-
-
The sparsest possible AVL tree with n nodes has height
-
-
h
 1.44log n
1.44log n
-
-
The worst case height of an AVL tree with n nodes is
-
-
1.44log n
Figure 5.3: Fibonacci trees
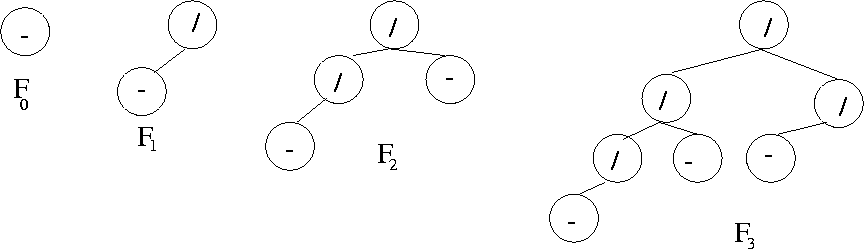 |
Figure 5.4: Rotations in a binary search tree
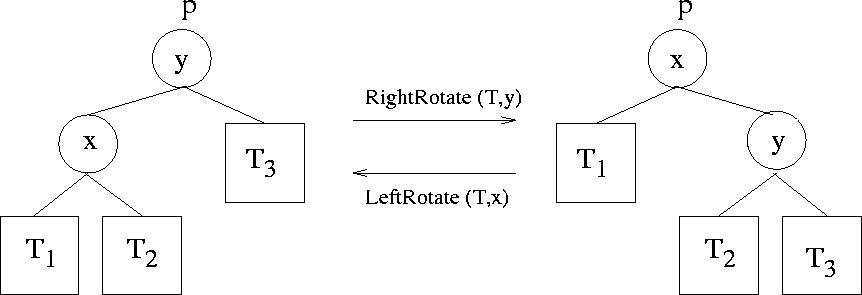 |



Next:5.1.2
AVL Trees: Insertions and DeletionsUp:5.1
AVL TreesPrevious:5.1
AVL Trees
eEL,CSA_Dept,IISc,Bangalore
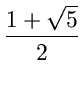

 1.44log| Fn|
1.44log| Fn|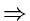
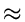 1.44log n
1.44log n