4.4 Binary Search Tree

• A prominent data structure used in many systems programming applications for representing and managing dynamic sets.
• Average case complexity of Search, Insert, and Delete Operations is O(log n), where n is the number of nodes in the tree.
• DEF: A binary tree in which the nodes are labeled with elements of an ordered dynamic set and the following BST property is satisfied: all elements stored in the left subtree of any node x are less than the element stored at x and all elements stored in the right subtree of x are greater than the element at x.
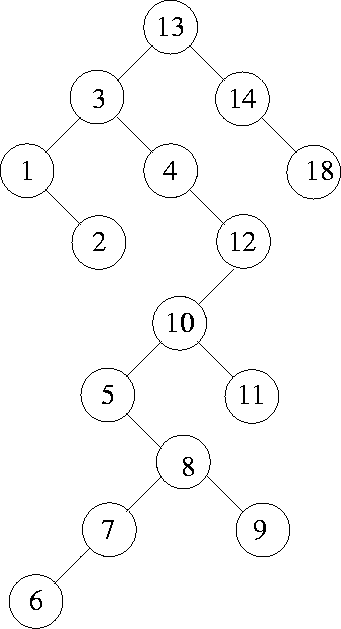
• An Example: Figure 4.14 shows a binary search tree. Notice that this tree is obtained by inserting the values 13, 3, 4, 12, 14, 10, 5, 1, 8, 2, 7, 9, 11, 6, 18 in that order, starting from an empty tree.
• Note that inorder traversal of a binary search tree always gives a sorted sequence of the values. This is a direct consequence of the BST property. This provides a way of sorting a given sequence of keys: first, create a BST with these keys and then do an inorder traversal of the BST so created.
• Note that the highest valued element in a BST can be found by traversing from the root in the right direction all along until a node with no right link is found (we can call that the rightmost element in the BST).
• The lowest valued element in a BST can be found by traversing from the root in the left direction all along until a node with no left link is found (we can call that the leftmost element in the BST).
• Search is straightforward in a BST. Start with the root and keep moving left or right using the BST property. If the key we are seeking is present, this search procedure will lead us to the key. If the key is not present, we end up in a null link.
• Insertion in a BST is also a straightforward operation. If we need to insert an element x, we first search for x. If x is present, there is nothing to do. If x is not present, then our search procedure ends in a null link. It is at this position of this null link that x will be included.
• If we repeatedly insert a sorted sequence of values to form a BST, we obtain a completely skewed BST. The height of such a tree is n - 1 if the tree has n nodes. Thus, the worst case complexity of searching or inserting an element into a BST having n nodes is O(n).

  

Figure 4.14: An example of a binary search tree

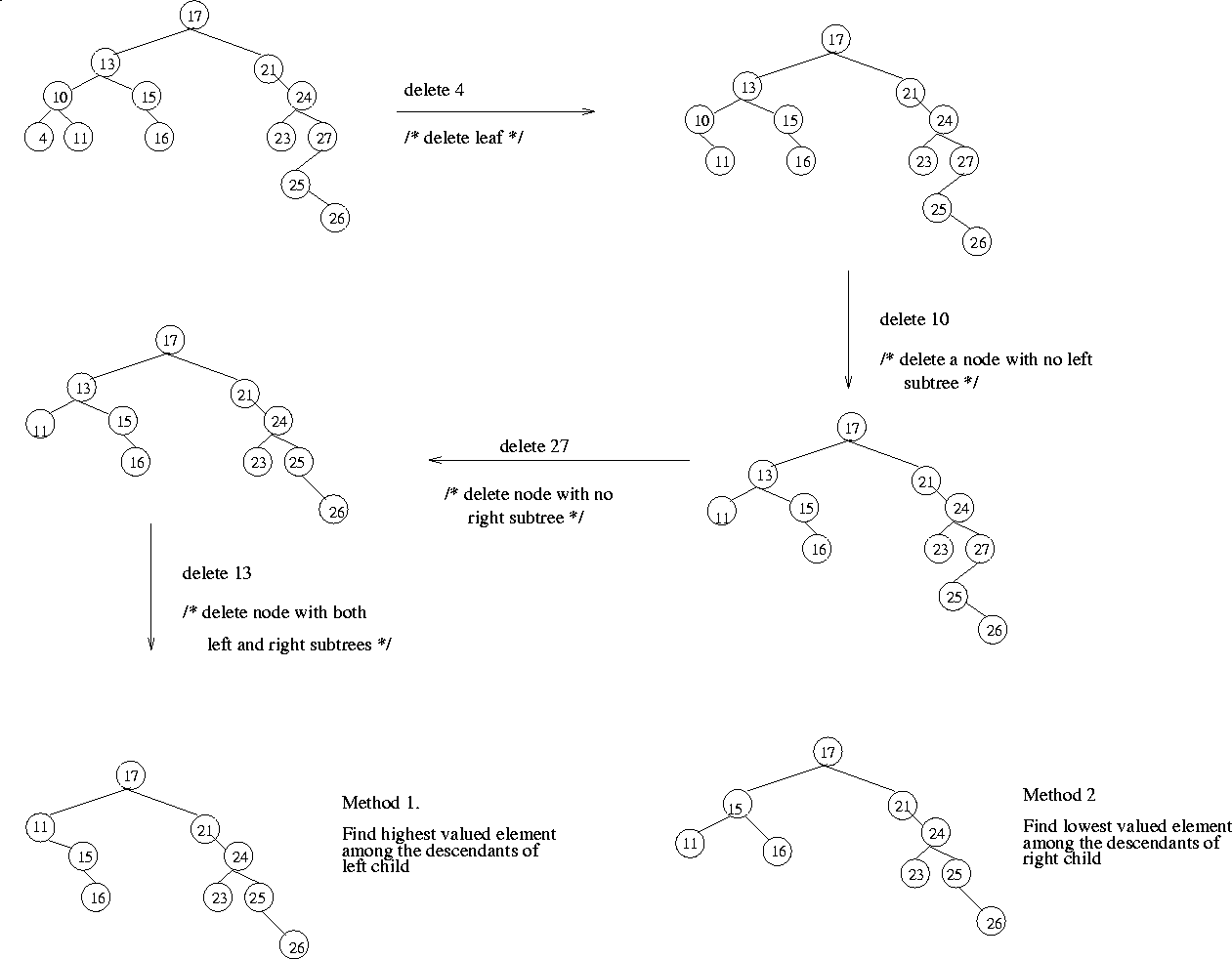
Deletion in BST

Let x be a value to be deleted from the BST and let X denote the node containing the value x. Deletion of an element in a BST again uses the BST property in a critical way. When we delete the node X containing x, it would create a "void" that should be filled by a suitable existing node of the BST. There are two possible candidate nodes that can fill this void, in a way that the BST property is not violated: (1). Node containing highest valued element among all descendants of left child of X. (2). Node containing the lowest valued element among all the descendants of the right child of X. In case (1), the selected node will necessarily have a null right link which can be conveniently used in patching up the tree. In case (2), the selected node will necessarily have a null left link which can be used in patching up the tree. Figure 4.15 illustrates several scenarios for deletion in BSTs.

  

Figure 4.15: Deletion in binary search trees: An example