


Next:4.5
Splay TreesUp:4.4
Binary Search TreePrevious:4.4
Binary Search Tree
4.4.1 Average Case Analysis of
BST Operations
RESULT
If we insert n random elements into an initially empty BST, then
the average path length from the root to a node is O(log n)
-
Note that the BST is formed by insertions only. Obviously the tree so formed
need not be complete.
-
We shall assume that all orders of n inserted elements are equally likely.
This means that any of the n! permutations is equally likely to be the
sequence of keys inserted.
| Let |
|
|
| P(n) |
= |
average path length in a BST with n nodes |
| |
|
(average number of nodes on the path from the root |
| |
|
to a node, not necessarily a leaf) |
| |
|
|
| Let |
|
|
| a |
= |
first element inserted. This will be the root of |
| |
|
the BST. Also this is equally likely to be the first, second |
| |
|
. . . , ith, . . . , or nth in the sorted order of
the |
| |
|
n elements. |
Note that P(0) = 0 and P(1) = 1. Consider a fixed i,
0  i
i n
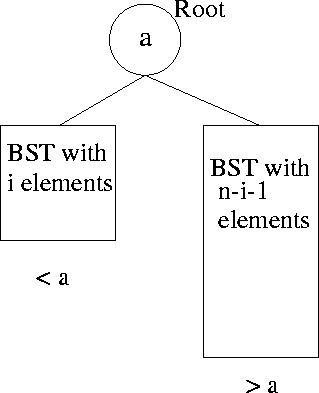
- 1. If i elements are less than a, the BST will look like in Figure
4.16.
n
- 1. If i elements are less than a, the BST will look like in Figure
4.16.
Figure 4.16: A typical binary search tree with n
elements
 |
-

-
Since all orders for the i small elements are equally likely and
likewise for the (n - i - 1) larger elements,
Average path length in the
-
left subtree = P(i)
-
right subtree = P(n - i - 1)
-

-
For a fixed i, let us compute the average path length of the above
tree.
-
Number of probes if the element a is being sought = 1
-
Average number of probes if an element from the LST is sought = 1+P(i)
-
Average number of probes if an element from the RST is sought = 1 + P(n
- i - 1)
-
Probability of seeking any of the n elements =
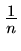
-
-
| |
= |
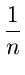  1
+ i(1 + P(i)) + (n - i - 1)(1 + P(n
- i - 1)) 1
+ i(1 + P(i)) + (n - i - 1)(1 + P(n
- i - 1))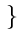 |
|
| |
= |
1 + 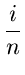 P(i)
+ P(i)
+  P(n
- i - 1) P(n
- i - 1) |
|
| |
= |
P(n, i), say. |
|
-

-
Observe that P(n) is given by
-
P(n) =
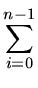 Prob{LST has $i$ nodes }P(n, i)
Prob{LST has $i$ nodes }P(n, i)
Since the probability that the LST has i elements which is the
same as the probability that a is the (i + 1th element (where i
= 0, 1,..., n - 1) = 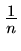 ,
we have
,
we have
| P(n) |
= |
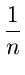 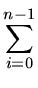 P(n, i)
P(n, i) |
|
| |
|
|
|
| |
= |
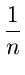 ![$\displaystyle \left\{\vphantom{\sum_{i=0}^{n-1} \space \left[1 + \frac{i}{n} P(i) +\frac{n-i-1}{n} P(n-i-1\right]}\right.$](img175.gif) 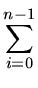  1
+ 1
+ 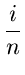 P(i)
+ P(i)
+  P(n
- i - 1 P(n
- i - 1![$\displaystyle \left.\vphantom{1 + \frac{i}{n} P(i) +\frac{n-i-1}{n} P(n-i-1}\right]$](img177.gif) ![$\displaystyle \left.\vphantom{\sum_{i=0}^{n-1} \space \left[1 + \frac{i}{n} P(i) +\frac{n-i-1}{n} P(n-i-1\right]}\right\}$](img178.gif) |
|
| |
|
|
|
| |
= |
1 + 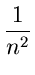 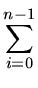  iP(i)
+ (n - i - 1)P(n - i - 1 iP(i)
+ (n - i - 1)P(n - i - 1![$\displaystyle \left.\vphantom{iP(i) +(n-i-1)P(n-i-1}\right]$](img181.gif) |
|
| |
|
|
|
| |
= |
1 + 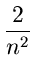 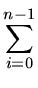 iP(i)
iP(i) |
|
since
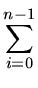 iP(i) =
iP(i) = 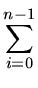 (n - i - 1)P(n - i - 1)
(n - i - 1)P(n - i - 1)
-

-
Thus the average path length in a BST satisfies the recurrence:
P(n) = 1 + 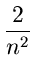
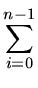 iP(i)
iP(i)
-

-
We shall show that P(n)
 1 + 4log n, by Induction.
1 + 4log n, by Induction.
Basis:
-
P(1) is known to be 1. Also the RHS = 1 for n = 1
Induction:
-
Let the result be true
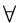 i < n. We shall show that the above is true for i
= n.
i < n. We shall show that the above is true for i
= n.
Consider
| P(n) |
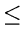 |
1 + 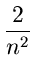 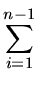 i(1 + 4log i)
i(1 + 4log i) |
|
| |
|
|
|
| |
= |
1 + 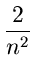 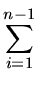 4ilogi +
4ilogi + 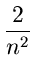 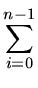 i
i |
|
| |
|
|
|
| |
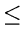 |
1 + 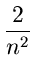 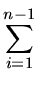 4ilogi +
4ilogi + 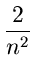 tex2html_image_mark>#tex2html_wrap_indisplay25297#� tex2html_image_mark>#tex2html_wrap_indisplay25297#�  since
since 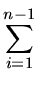 i
i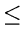  |
|
Thus
P(n) 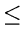 2 +
2 + 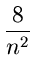
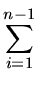 ilog i
ilog i
Now
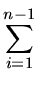 ilog i
ilog i |
= |
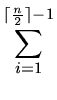 ilogi +
ilogi + 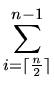 ilog i
ilog i |
|
| |
|
|
|
| |
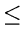 |
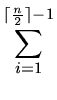 ilog
ilog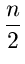 +
+ 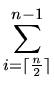 ilog n
ilog n |
|
| |
|
|
|
| |
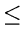 |
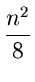 log log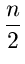 +
+ 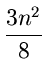 log
n log
n |
|
| |
|
|
|
| |
= |
 logn
- logn
- 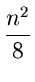 |
|
Therefore
P(n) 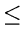 2 +
2 + 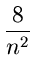
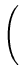
 log
-
log
- 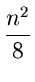
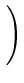 = 1 + 4log n
= 1 + 4log n
A more careful analysis can be done and it can be shown that
P(n) 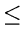 1 + 1.4log n
1 + 1.4log n



Next:4.5
Splay TreesUp:4.4
Binary Search TreePrevious:4.4
Binary Search Tree
eEL,CSA_Dept,IISc,Bangalore
![]() i
i![]() n
- 1. If i elements are less than a, the BST will look like in Figure
4.16.
n
- 1. If i elements are less than a, the BST will look like in Figure
4.16.

 P(n
- i - 1)
P(n
- i - 1) P(n
- i - 1
P(n
- i - 1![]() 2 +
2 + ![]()
![]() ilog i
ilog i
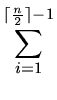 ilogi +
ilogi + 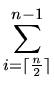 ilog i
ilog i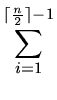 ilog
ilog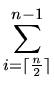 ilog n
ilog n![]() 2 +
2 + ![]()
![]()
![]() log
-
log
- ![]()
![]() = 1 + 4log n
= 1 + 4log n
![]() 1 + 1.4log n
1 + 1.4log n