


Next: 4.4 Binary Search Tree
Up: 4.3 An Application of Binary Trees: Huffman Code Construction
Previous: 4.3.1 Implementation
- 1.
- while (there is more than one tree in the forest) do {
- 2.
- i = index of tree in forest with smallest weight ;
- 3.
- j = index of tree in forest with second smallest weight ;
- 4.
- create a new node with
-
- lchild = forest [i].root ;
-
- rchild = forest [j].root ;
- 5.
- replace tree i in forest by a tree with root as
new node, with
-
- weight = forest [i]
 weight + forest[j]
weight + forest[j]
 weight ;
weight ;
- 6.
- delete tree j from forest
-
- }
Line (4)
 increases the number of cells of the array
tree.
Lines (5) and (6)
increases the number of cells of the array
tree.
Lines (5) and (6)
 decrease the number of utilized
cells of forest.
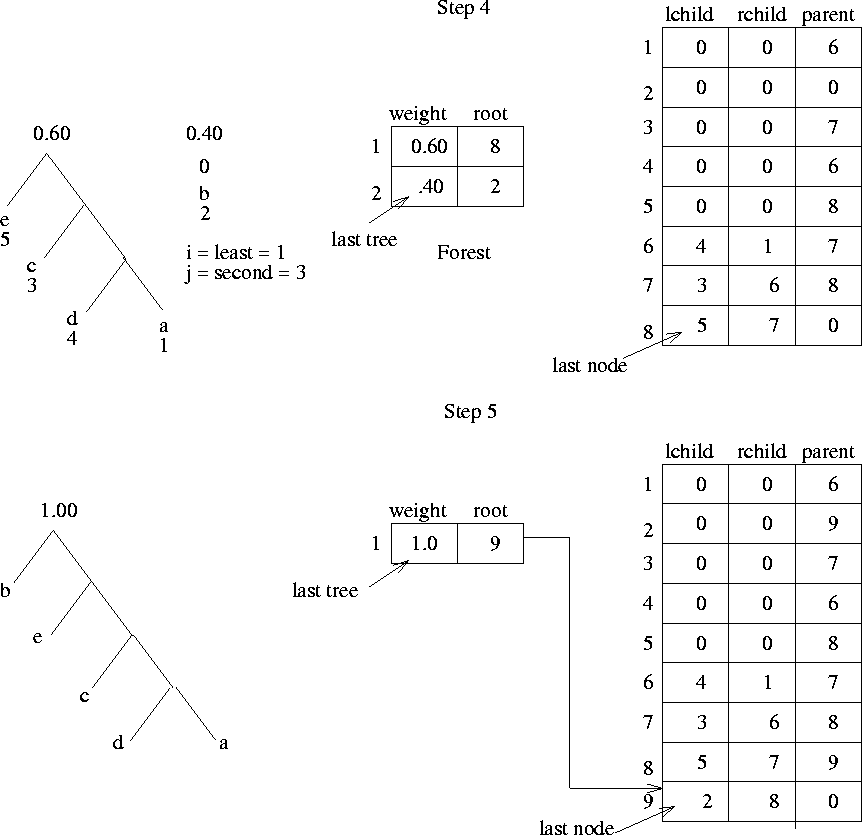
Figures 4.11, 4.12, and
4.13 illustrate different steps of the above
algorithm for our example problem.
decrease the number of utilized
cells of forest.
Figures 4.11, 4.12, and
4.13 illustrate different steps of the above
algorithm for our example problem.
Figure 4.12:
Step 2 and Step 3
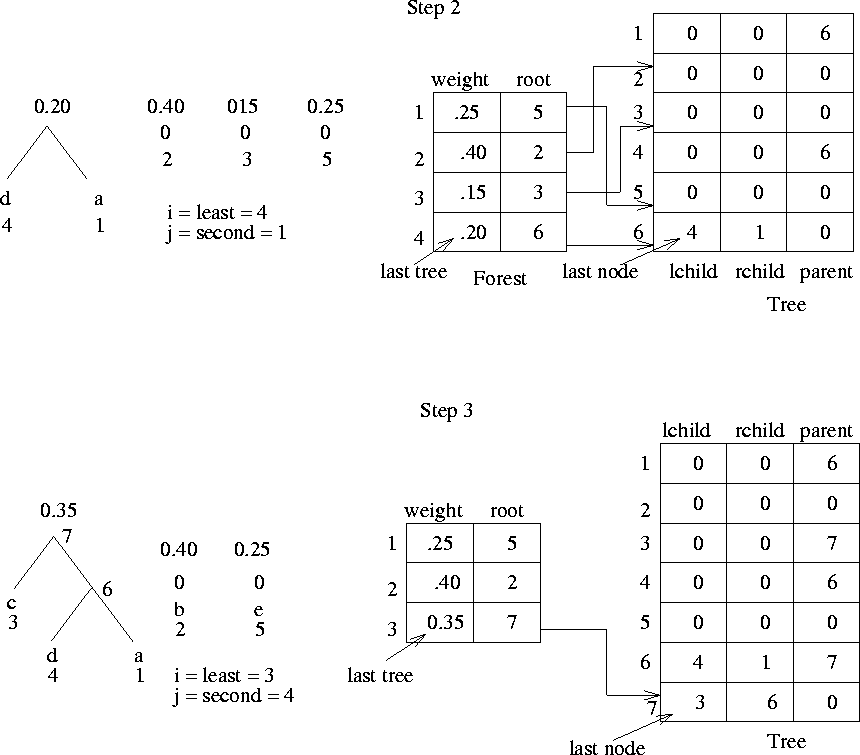 |
Figure 4.13:
Step 4 and Step 5
 |



Next: 4.4 Binary Search Tree
Up: 4.3 An Application of Binary Trees: Huffman Code Construction
Previous: 4.3.1 Implementation
eEL,CSA_Dept,IISc,Bangalore
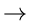 weight + forest[j]
weight + forest[j]
 weight ;
weight ;