


Next:7.2.3
All Pairs Shortest Paths Problem: Floyd's AlgorithmUp:7.2
Shortest Paths ProblemPrevious:7.2.1
Single Source Shortest Paths Problem: Dijkstra's Algorithm
7.2.2 Dynamic Programming Algorithm
-
REF.
-
Richard Bellman. Dynamic Programming. Princeton University Press,
1957.
-
REF.
-
Richard Bellman. On a routing problem. Quarterly of Applied Mathematics,
Volume 16, Number 1, pp. 87-90, 1958.
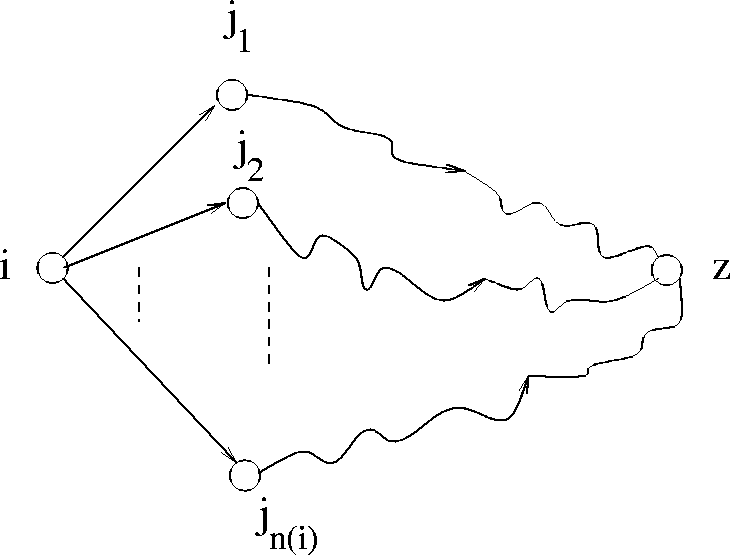
Consider a directed acyclic graph (digraph without cycles) with nonnegative
weights on the directed arcs.
Given a destination vertex z, the problem is to find a shortest cost
path from each vertex of the digraph. See Figure 7.6.
Let
| C(i, j) |
= |
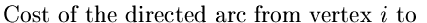 |
|
| |
|
 |
(7.8) |
| J(i) |
= |
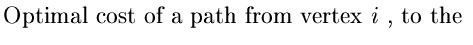 |
(7.9) |
| |
|
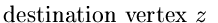 |
|
J(i) Satisfies :
J(z) = 0
and if the optimal path from i to z traverses the link (i, j) then
J(i) = C(i, j) + J(j)
Figure 7.6: Principle of dynamic programming
 |
Suppose that for each vertex j such that the link (i, j) exists, the
optimal cost J(j) is known. Then, the principle of DP immediately implies:
J(i) = 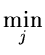 [C(i, j) + J(j)]
A DP algorithm based on the above observations:
[C(i, j) + J(j)]
A DP algorithm based on the above observations:
-
1.
-
Set J(z) = 0. At this point, this is the only node whose
cost has been computed.
-
2.
-
Consider vertices i
 V
such that
V
such that
-
J(i) has not yet been found
-
for each vertex j such that a link (i, j) exists,
J(j) is already computed
Assign J(i) according to
J(i) = 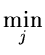 [C(i,
j) + J(j)]
[C(i,
j) + J(j)]
-
3.
-
Repeat Step 2 until all vertices have their optimal costs computed.
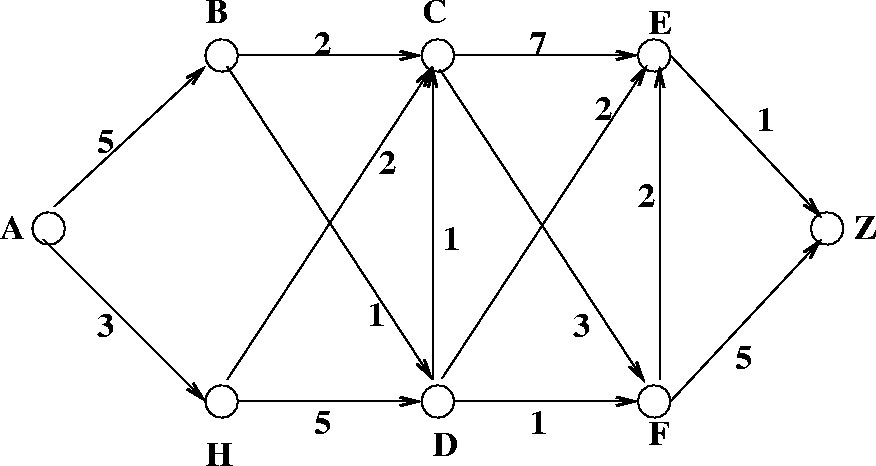
Example: Consider the digraph in Figure 7.7
Figure 7.7: An example digraph to illustrate dynamic programming
 |
-
Step 1.
-
J(Z) = 0
-
Step 2.
-
E is the only vertex such that J(j) is known
 I>j
such that C(E, j)
I>j
such that C(E, j) 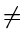 0
0
J(E) = C(E, Z) + J(Z)
= 1
-
Step 3.
-
Select F.
| J(F) |
= |
min 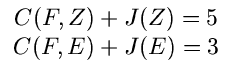  |
(7.10) |
| |
= |
min(5, 3) = 3 |
|
This yields the optimal path F E
E Z.
Z.
-
Step 4.
-
Select C.
| J(C) |
= |
min   |
(7.11) |
| |
= |
min(8, 6) = 6 |
|
This yields the optimal path C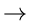 F
F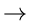 E
E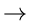 Z.
Z.
-
Step 5.
-
Select D
J(D) = min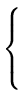
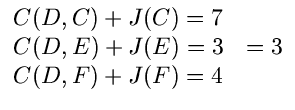
 This yields the optimal path D
This yields the optimal path D E
E Z.
Z.
Eventually, we get all the optimal paths and all the optimal costs.
Complexity of the Algorithm
-
It is easy to see that the algorithm has a worst case complexity of
O(n2),
where n is the number of vertices.
-
Limitation of the algorithm
-
doesn't work if there are cycles in the digraph.



Next:7.2.3
All Pairs Shortest Paths Problem: Floyd's AlgorithmUp:7.2
Shortest Paths ProblemPrevious:7.2.1
Single Source Shortest Paths Problem: Dijkstra's Algorithm
eEL,CSA_Dept,IISc,Bangalore

![]() [C(i,
j) + J(j)]
[C(i,
j) + J(j)]

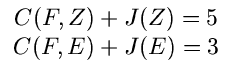
![]() E
E![]() Z.
Z.
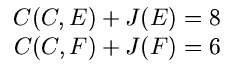
![]() F
F![]() E
E![]() Z.
Z.
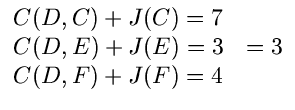
![]()