| tex2html_deferredGiven | |||
| tex2html_deferredGiven | |||
Floyd's Algorithm
| A[i, j] | = | C[i, j] if i |
(7.12) |
| = | 0 if i = j |
Note that C[i, j] is taken as ![]() if there is no directed arc from ito j.
if there is no directed arc from ito j.
| Ak - 1[i, j] | = | (7.13) | |
| (7.14) | |||
See Figure 7.8
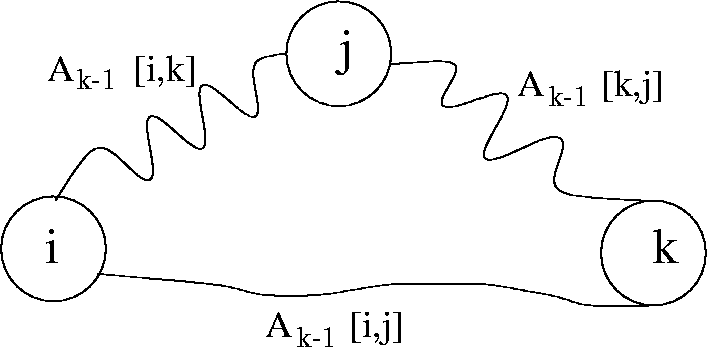 |
![$\displaystyle \begin{array}{l} A_{k-1} [i,j] \\ A_{k-1}[i,k] +A_{k-1}[k,j]\end{array}$](img353.gif)
{ int i, j, k;
{ for(i = 0, i![]() n
- 1;i + +)
n
- 1;i + +)
for(j = 0;j![]() n
- 1, j + +)
n
- 1, j + +)
A[i, j] = C[i, j];
for(i = 0;i![]() n
- 1;i + +)
n
- 1;i + +)
A[i, i] = 0;
for(k = 0;k![]() n
- 1;k + +);
n
- 1;k + +);
{
for(i = 0;i![]() n
- 1;i + +)
n
- 1;i + +)
{
for(j = 0;j![]() n
- 1, j + +)
n
- 1, j + +)
if(A[i, k] + A[k, j] < A[i, j])
A[i, j] = A[i, k] + A[k, j]
}
}
}
}
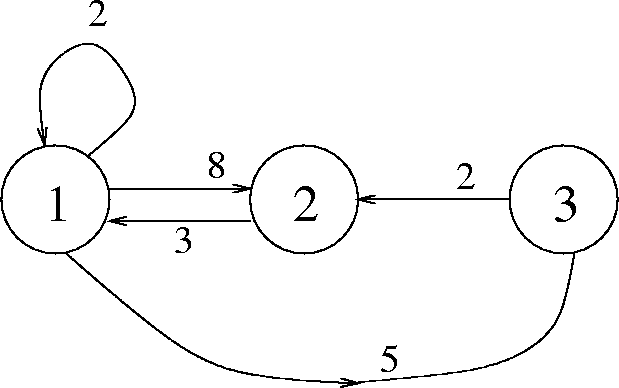 |
Example: See Figure 7.9.
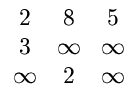
| A0 | = | 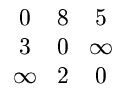 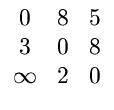 |
(7.15) |
| A2 | = | 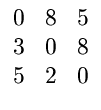 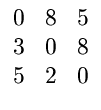 |