7.2.1 Single Source Shortest Paths Problem: Dijkstra's Algorithm

REF.

E.W. Dijkstra. A note on two problems in connection with graphs. Numerische Mathematik, Volume 1, pp. 269-271, 1959.

• Greedy algorithm
• It works by maintaining a set S of ``special'' vertices whose shortest distance from the source is already known. At each step, a ``non-special'' vertex is absorbed into S.
• The absorption of an element of V - S into S is done by a greedy strategy.
• The following provides the steps of the algorithm.

Let

V = {1, 2,..., n} and source = 1 (7.1)

$$\mbox{Cost of the arc $(i, j)$\space if the arc $(i,j)$\space exists;otherwise $\infty$ }$$ C[i, j] =

{

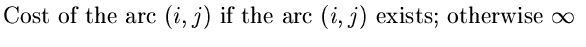        S= { 1 };

            for (i = 2; i < n; i++)

                D[i] = C[1,i];

            for (i=1; i < = n-1; i++)

    {

                choose a vertex w $\in$ V-S such that D[w] is a minimum;

                S = S $\cup$ {w };

                for each vertex v $\in$ V-S

                     D[v] = min (D[v], D[w] + C[w, v])

    }

}

• The above algorithm gives the costs of the shortest paths from source vertex to every other vertex.
• The actual shortest paths can also be constructed by modifying the above algorithm.

Theorem: Dijkstra's algorithm finds the shortest paths from a single source to all other nodes of a weighted digraph with positive weights.

Proof: Let V = 1, 2, ..., n and 1 be the source vertex. We use mathematical induction to show that

(a)

If a node i ( $\neq$ 1) $\in$S, then D[i] gives the length of the shortest path from the source to i.

(b)

if a node i$\notin$S, then D[i] gives the length of the shortest special path from the source to i.

Basis: Initially S = 1 and hence (a) is vacuously true. For i$\in$S, the only special path from the source is the direct edge if present from source to i and D is initialized accordingly. Hence (b) is also true.

Induction for condition (a)

• The induction hypothesis is that both (a) and (b) hold just before we add a new vertex v to S.
• For every node already in S before adding v, nothing changes, so condition (a) is still true.
• We have to only show (a) for v which is just added to S.

 

 
 


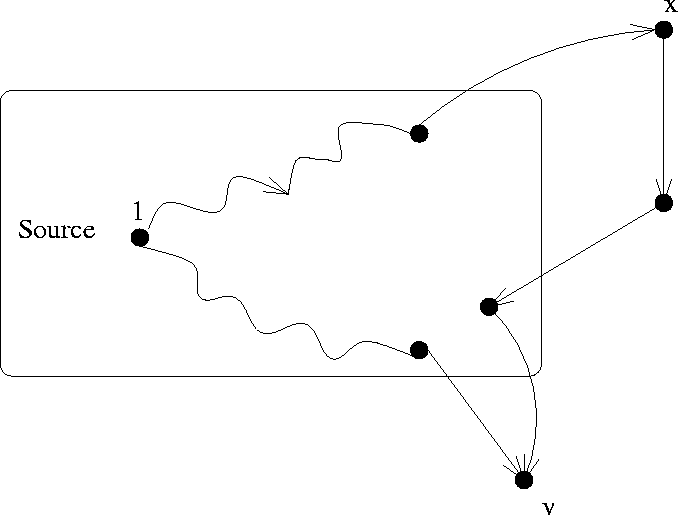
Figure 7.4: The shortest path to v cannot visit x


• Before adding it to S, we must check that D[v] gives the length of the shortest path from source to v. By the induction hypothesis, D[v] certainly gives the length of the shortest special path. We therefore have to verify that the shortest path from the source to v does not pass through any nodes that do not belong to S.
• Suppose to the contrary. That is, suppose that when we follow the shortest path from source to v, we encounter nodes not belonging to S. Let x be the first such node encountered (see Figure 7.4 ). The initial segment of the path from source to x is a special path and by part (b) of the induction hypothesis, the length of this path is D[x]. Since edge weights are no-negative, the total distance to v via x is greater than or equal to D[x]. However since the algorithm has chosen v ahead of x, D[x] 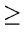$\geq$D[v]. Thus the path via x cannot be shorter than the shortest special path leading to v.

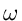
Induction step for condition (b): Let $\omega$$\neq$v and $\omega$$\in$S. When v is added to S, these are two possibilities for the shortest special path from source to w:

1.

It remains as before

2.

It now passes through v ( and possibly other nodes in S)

In the first case, there is nothing to prove. In the second case, let y be the last node of S visited before arriving at w. The length of such a path is D[y] + C[y,w].

• At first glance, to compute the new value of d[w], it looks as if we should compare the old value of D[w] with D[y] + C[y,w] for every y $\in$ S (including v)
• This comparison was however made for all y $\in$ S except v, when y was added to S in the algorithm. Thus the new value of D[w] can be computed simply by comparing the old value with D[v] + C[v,w]. This the algorithm does.

When the algorithm stops, all the nodes but one are in S and it is clear that the vector D[1], D[2], ..., D[n]) contains the lengths of the shortest paths from source to respective vertices.

Example: Consider the digraph in Figure 7.5.
 

Figure 7.5: A digraph example for Dijkstra's algorithm

Initially:

S = {1}  D[2] = 10  D[3] = $$\infty$$ D[4] = 30  D[5] = 100

Iteration 1

Select w = 2, so that S = {1, 2}

$$\infty$$ D[3] = (7.2)

D[4] = min(30, D[2] + C[2, 4]) = 30 (7.3)

D[5] = min(100, D[2] + C[2, 5]) = 100

Iteration 2

Select w = 4, so that S = {1, 2, 4}

D[3] = min(60, D[4] + C[4, 3]) = 50 (7.4)

D[5] = min(100, D[4] + C[4, 5]) = 90

Iteration 3

Select w = 3, so that S = {1, 2, 4, 3}

D[5] = min(90, D[3] + C[3, 5]) = 60

Iteration 4

Select w = 5, so that S = {1, 2, 4, 3, 5}

D[2] = 10 (7.5)

D[3] = 50 (7.6)

D[4] = 30 (7.7)

D[5] = 60

Complexity of Dijkstra's Algorithm

With adjacency matrix representation, the running time is O(n2) By using an adjacency list representation and a partially ordered tree data structure for organizing the set V - S, the complexity can be shown to be

O(elog n) where e is the number of edges and n is the number of vertices in the digraph.