6.1 Binary Heaps

Heaps (occasionally called as partially ordered trees) are a very popular data structure for implementing priority queues.

• A heap is either a min-heap or a max-heap. A min-heap supports the insert and deletemin operations while a max-heap supports the insert and deletemax operations.
• Heaps could be binary or d-ary. Binary heaps are special forms of binary trees while d-ary heaps are a special class of general trees.
• Binary heaps were first introduced by Williams in 1964.

REF. J.W.J. Williams. Algorithm 232: Heapsort. Communications of the ACM, Volume 7, 1964, pp 347-348

We discuss binary min-heaps. The discussion is identical for binary max-heaps.

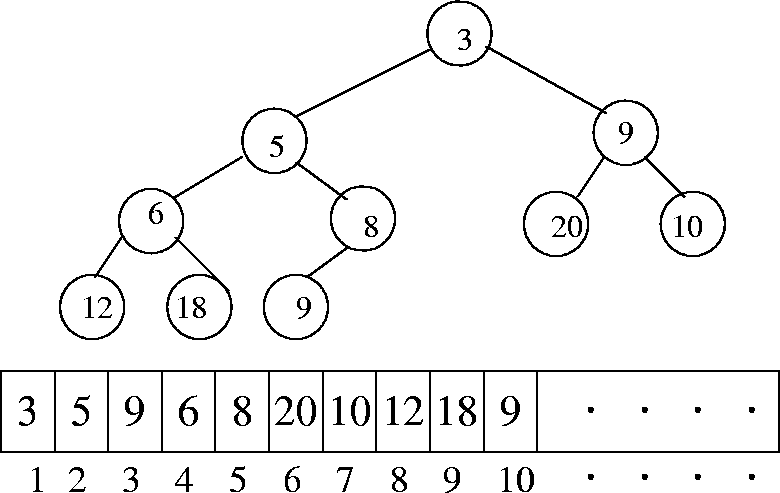
DEF. A binary heap is a complete binary tree with elements from a partially ordered set, such that the element at every node is less than (or equal to) the element at its left child and the element at its right child. Figure 6.1 shows and example of a heap.

Figure 6.1: An example of a heap and its array representation

• Since a heap is a complete binary tree, the elements can be conveniently stored in an array. If an element is at position i in the array, then the left child will be in position 2i and the right child will be in position 2i + 1. By the same token, a non-root element at position i will have its parent at position $\lfloor$ ${\frac{i}{2}}$ $\rfloor$
• Because of its structure, a heap with height k will have between 2^kand 2^{k + 1} - 1 elements. Therefore a heap with n elements will have height = $\lfloor$log₂ n $\rfloor$
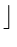
• Because of the heap property, the minimum element will always be present at the root of the heap. Thus the findmin operation will have worst-case O (1) running time.