5.2.1 Height of a Red-Black Tree

Result 1

In a RBT, no path from a node x to a leaf is more than twice as long as any other path from x to a leaf.

Let bh(x) be the black height of x. Then the length of a longest path from x to a leaf 

                    = 2bh(x)  {a path on which red and black nodes alternate}

Length of the shortest possible path from x to a leaf 

                    bh(x)  {a path that only contains blacks}

Hence the result.

Result 2

A red-black tree with n internal nodes has height at most

                   2log(n + 1)

Consider any node x and the subtree rooted at x. We will first show that this subtree has at least

                   2^bh(x) - 1  internal nodes
We do this by induction on the height of x. If h(x) = 0, bh(x) = 0, x is leaf and hence the subtree has no internal nodes, as corroborated by

                    2⁰ - 1 = 0

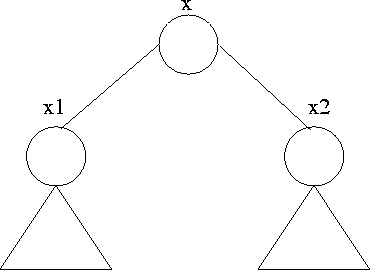
Let h(x) > 0 and let x1 and x2 be its two children (Figure 5.11)
 
 

Figure 5.11: A simple red-black tree

Note that h(x1), h(x2) are both $\leq$h(x) - 1. Assume the result to be true for x1 and x2. We shall show the result is true for x.

Now,

$$\leq \geq$$ bh(x₁)

$$\leq \geq$$ bh(x₂)

Therefore, the tree with root x1 has at least 

                    $$\left(\vphantom{2^{bh(x)-1} - 1}\right.$$2^{bh(x) - 1} - 1$$\left.\vphantom{2^{bh(x)-1} - 1}\right)$$  internal nodes
whereas the tree with root x2 has at least 

                    $$\left(\vphantom{2^{bh(x)-1} - 1}\right.$$2^{bh(x) - 1} - 1$$\left.\vphantom{2^{bh(x)-1} - 1}\right)$$  internal nodes
Thus the tree with root x has at least

                        1 + 2^{bh(x) - 1} - 1 + 2^{bh(x) - 1} - 1 = $$\left(\vphantom{2^{bh(x)} - 1}\right.$$2^bh(x) - 1$$\left.\vphantom{2^{bh(x)} - 1}\right)$$  $$\Leftarrow$$   internal nodes
To complete the proof, let h be the height of the tree. Then

                        bh (root) $$\geq$$$${\frac{h}{2}}$$
Thus

$$\geq$$ n/TD>  2^h/2 - 1

$$\Rightarrow \geq$$  2log(n + 1)