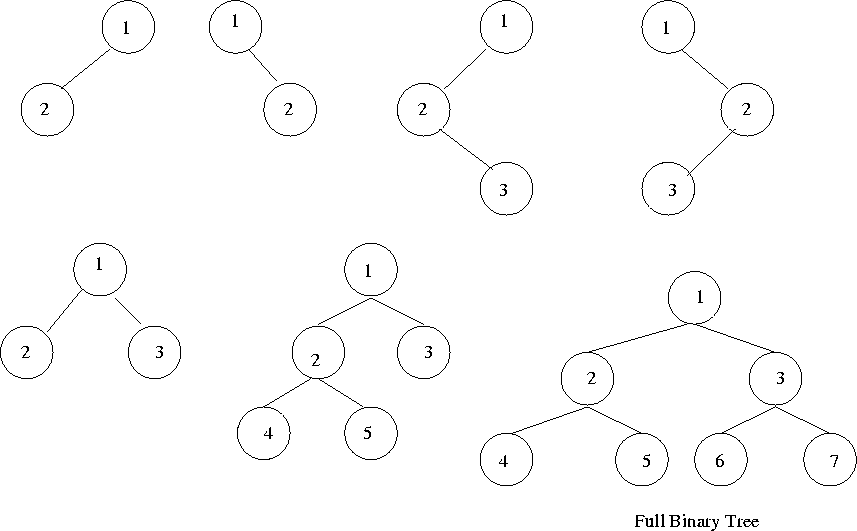
max # of leaves = 2h
max # of nodes = 2h + 1 - 1
 |
 |
= number of stack-realizable permutations of length n
= number of well-formed parentheses (with n left parentheses and n right parentheses)
= ![]()
![]()
![]()
![]()
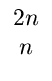
![]()
![]()
max # of leaves = 2h
max # of nodes = 2h + 1 - 1
 |
 |
= number of stack-realizable permutations of length n
= number of well-formed parentheses (with n left parentheses and n right parentheses)
= ![]()
![]()
![]()
![]()
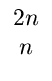
![]()
![]()
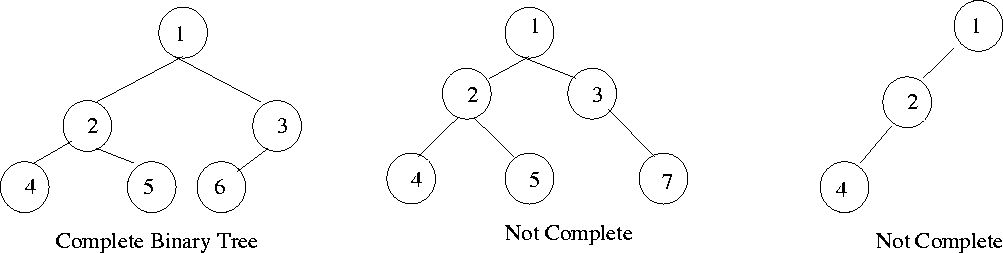 |
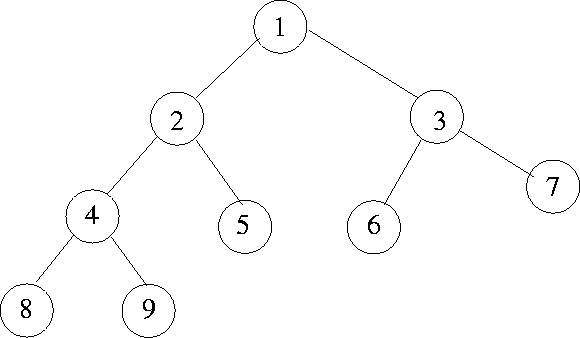
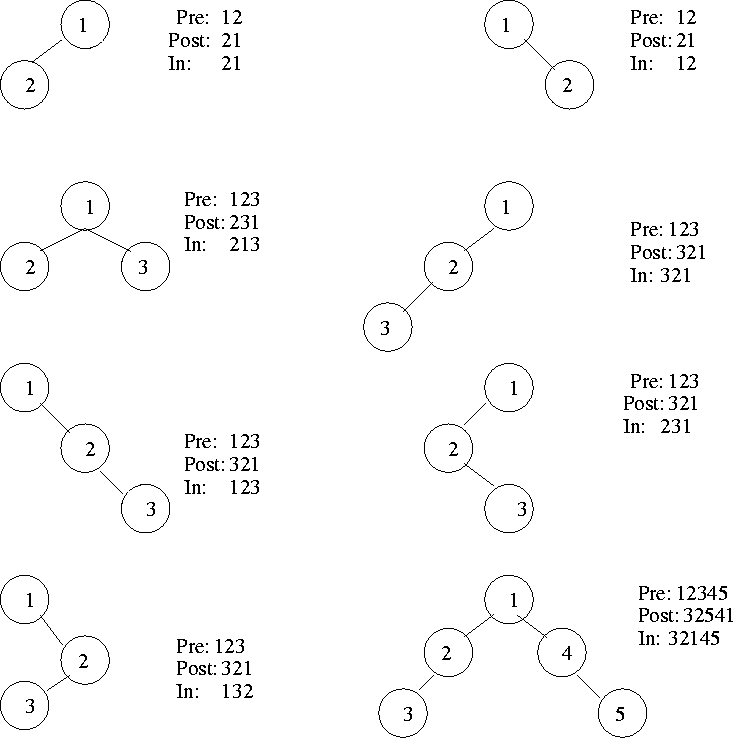
Binary Tree Traversal:
Visit root, visit left subtree in preorder, visit right subtree
in preorder
Visit left subtree in postorder, right subtree in postorder, then
the root
Visit left subtree in inorder, then the root, then the right subtree
in inorder
 |
Data Structures for Binary Trees:
item-type info ;
struct node-tag * left ;
struct node-tag * right ;
} node-type ;
node-type * root ; /* pointer to root */
node-type * p ; /* temporary pointer */
void preorder(node-type * root)
{
if (root) {
visit (root) ;
preorder (root ![]() left) ;
left) ;
preorder (root ![]() right) ;
right) ;
}
}
void inorder (node-type * root)
{
if (root) {
inorder (root ![]() left) ;
left) ;
visit (root) ;
inorder (root ![]() right) ;
right) ;
}
}
void postorder (node-type * root)
{
if (root) {
postorder (root ![]() left) ;
left) ;
postorder (root ![]() right) ;
right) ;
visit (root) ;
}
}