4.1.2 Preorder, Inorder, Postorder

  $\mbox{$\bullet$}$

If a tree is null, then the empty list is the preorder, inorder, and postorder listing of T

  $\mbox{$\bullet$}$

If T comprises a single node, that node itself is the preorder, inorder, and postorder list of T

  $\mbox{$\bullet$}$

Otherwise

1.

The preorder listing of T is the root of T, followed by the nodes of T₁ in preorder, . . . , and the nodes of T_k in preorder.

2.

The inorder listing of T is the nodes of T₁ in inorder, followed by the root r, followed by the nodes of T₂ in inorder, . . . , and the nodes of T_k in inorder.

3.

The postorder listing of T is the nodes of T₁ in postorder, . . . , the nodes of T_k in postorder, all followed by the root r.

  $\mbox{$\bullet$}$

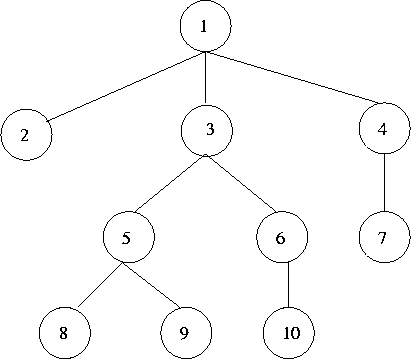
Example: see Figure 4.2.

Preorder 1,2,3,5,8,9,6,10,4,7

Postorder 2,8,9,5,10,6,3,7,4,1

Inorder 2,1,8,5,9,3,10,6,7,4

  $\mbox{$\bullet$}$

Note that the order of appearance of the leaves is the same in all the three schemes. This is true in general.

  

Figure 4.2: Example of a general tree