4.1.1 Definitions

We shall first present some definitions and then introduce the Tree ADT.

• Tree:

  1.

  A single node is a tree and this node is the root of the tree.

  2.

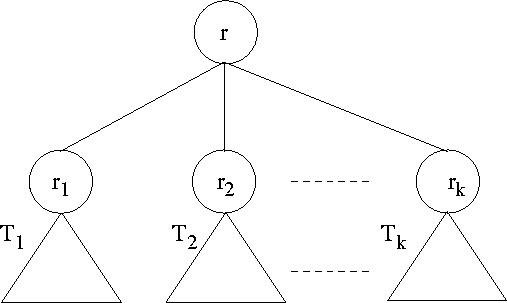
  Suppose r is a node and T₁, T₂,..., T_k are trees with roots r₁, r₂,..., r_k, respectively, then we can construct a new tree whose root is r and T₁, T₂,..., T_k are the subtrees of the root. The nodes r₁, r₂,..., r_k are called the children of r.

  
  

    

  Figure 4.1: Recursive structure of a tree

  
  
  

  See Figure 4.1. Often, it is convenient to include among trees, the null tree, which is a tree with no nodes.

• Path

  A sequence of nodes n₁, n₂,..., n_k, such that n_i is the parent of n_{i + 1} for i = 1, 2,..., k - 1. The length of a path is 1 less than the number of nodes on the path. Thus there is a path of length zero from a node to itself.

• Siblings

  The children of a node are called siblings of each other.

• Ancestor and Descendent

  If there is a path from node a to node b, then

  a is called an ancestor of b

  b is called a descendent of a

  If a $\neq$ b, then a is a proper ancestor and b is a proper descendent.

• Subtree

  A subtree of a tree is a node in that tree together with all its descendents.

• Height

  The height of a node in a tree is the length of a longest path from the node to a leaf. The height of a tree is the height of its root.

• Depth

  The depth of a node is the length of the unique path from the root to the node.

• Tree Traversal

  This is a systematic way of ordering the nodes of a tree. There are three popular schemes (many other schemes are possible):

  1.

  Preorder

  2.

  Inorder

  3.

  Postorder

  All these are recursive ways of listing or visiting all the nodes (each node exactly once)