3.8.1 Initialization:

An element NIL is allocated and given a key greater than any legal key. All levels of all lists are terminated with NIL. A new list is initialized so that the level of list = maxlevel and all forward pointers of the list's header point to NIL

Search:

We search for an element by traversing forward pointers that do not overshoot the node containing the element being searched for. When no more progress can be made at the current level of forward pointers, the search moves down to the next level. When we can make no more progress at level 1, we must be immediately in front of the node that contains the desired element (if it is in the list).

Insertion and Deletion:

• Insertion and deletion are through search and splice
• update [i] contains a pointer to the rightmost node of level i or higher that is to the left of the location of insertion or deletion.
• If an insertion generates a node with a level greater than the previous maximum level, we update the maximum level and initialize appropriate portions of update list.
• After a deletion, we check to see if we have deleted the maximum level element of the list and if so, decrease the maximum level of the list.
• Figure 3.9 provides an example of Insert and Delete. The pseudocode for Insert and Delete is shown below.

    search (list, searchkey);

            { x = list $\rightarrow$ header; for (i = list $\rightarrow$ level; i $\geq$ 1; i - -) {

                while (x$\rightarrow$ forward[i] $\rightarrow$ key < searchkey)

                x = x $\rightarrow$ forward[i];

        }

                x = x $\rightarrow$ forward[i];

            if (x $\rightarrow$ key = searchkey) return (true)

                else return false;

    }
 
 

Figure 3.9: A skip list

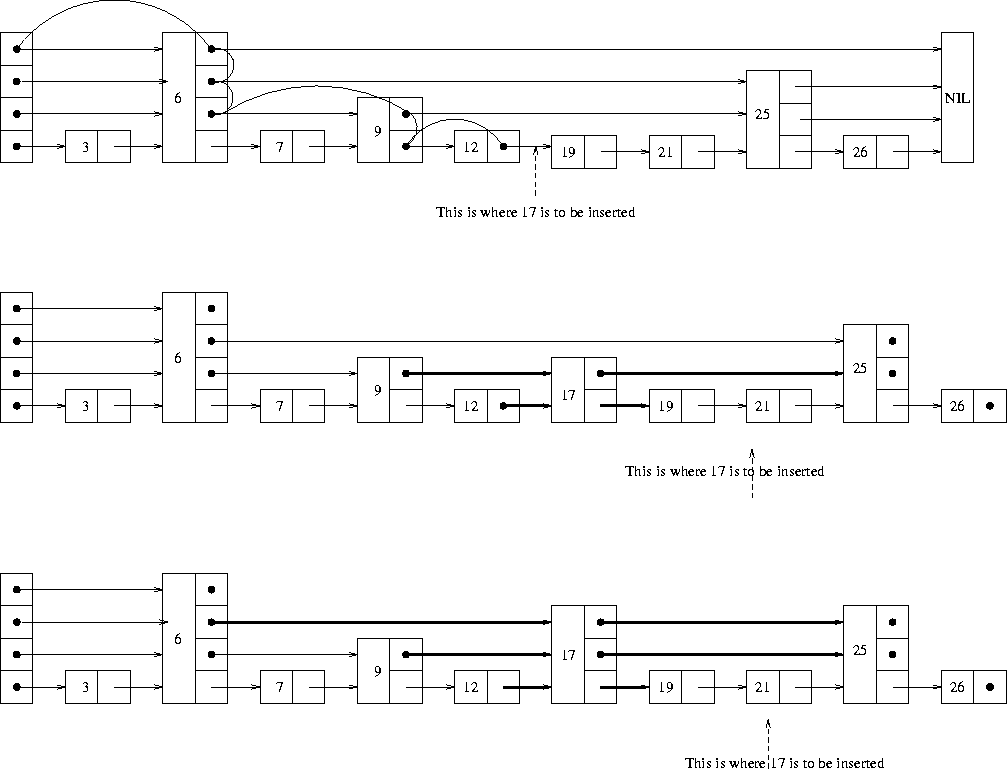    insert (list, searchkey);

            { x = list $\rightarrow$ header ;

                for (i = list $\rightarrow$ level; i $\geq$ 1; i - -) {

                    while (x $\rightarrow$ forward[i] $\rightarrow$ key < searchkey)

                x = x $\rightarrow$ forward[i];

                update[i] = x

        }

            x = x $\rightarrow$ forward[1];

            if (x $\rightarrow$ key = searchkey) return (``key already present'')

                else {

            newLevel = randomLevel();

                if newLevel > list $\rightarrow$ level {

                    for (i = list $\rightarrow$ level + 1; i $\leq$newLevel; i ++ )

                update[i] = list $\rightarrow$ header;

        }

            x = makenode(newLevel, searchkey);

                for (i = 1, i $\leq$ newLevel; i++) {

            x $\rightarrow$ forward[i] = update[i] $\rightarrow$ forward[i];

            update[i] $\rightarrow$ forward[i] = x

        }

}}

    delete (list, searchkey);

        { x = list $\rightarrow$ header ;

                for (i = list $\rightarrow$ level; i $\geq$ 1; i - ) {

                    while (x $\rightarrow$ forward[i] $\rightarrow$ key <searchkey)

            x = x $\rightarrow$ forward[i];

                    update[i] = x

        }

            x = x $\rightarrow$ forward[1];

                if (x $\rightarrow$ key = searchkey) {

                    for (i = 1; i $\leq$ list $\rightarrow$ level; i ++) {

                if (update[i] $\rightarrow$ forward[i] $\neq$ x) break;

                if (update[i] $\rightarrow$ forward[i] = x $\rightarrow$forward[i];

}

        free(x)

            While (( list $\rightarrow$ 1) &&

                (list $\rightarrow$ header $\rightarrow$ forward [list+level] = NIL))

                            list $\rightarrow$ level = list $\rightarrow$ level - 1