Next: 3.8.1 Initialization: Up: 3. Dictionaries Previous: 3.7 Hash Table Restructuring

3.8 Skip Lists

REF.: William Pugh. Skip Lists: A probabilistic alternative to balanced trees. Communications of the ACM, Volume 33, Number 6, pp. 668-676, 1990.

Skip lists use probabilistic balancing rather than strictly enforced balancing.
Although skip lists have bad worst-case performance, no input sequence consistently produces the worst-case performance (like quicksort).
It is very unlikely that a skip list will be significantly unbalanced. For example, in a dictionary of more than 250 elements, the chance is that a search will take more than 3 times the expected time $\leq$ 10^-6.
Skip lists have balance properties similar to that of search trees built by random insertions, yet do not require insertions to be random.

**Figure 3.4:** A singly linked list
$\begin{figure} \centerline{\psfig{figure=figures/Flist0.ps}} \end{figure}$

Consider a singly linked list as in Figure 3.4. We might need to examine every node of the list when searching a singly linked list.

Figure 3.5 is a sorted list where every other node has an additional pointer, to the node two ahead of it in the list. Here we have to examine no more than 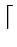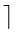$\lceil$ ${\frac{n}{2}}$ $\rceil$ +1 nodes.

**Figure 3.5:** Every other node has an additional pointer
$\begin{figure} \centerline{\psfig{figure=figures/Flist1.ps}} \end{figure}$

**Figure 3.6:** Every second node has a pointer two ahead of it
$\begin{figure} \centerline{\psfig{figure=figures/Flist2.ps}} \end{figure}$

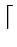
In the list of Figure 3.6, every second node has a pointer two ahead of it; every fourth node has a pointer four ahead if it. Here we need to examine no more than 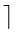$\lceil$ ${\frac{n}{4}}$ $\rceil$ + 2 nodes.

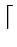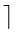In Figure 3.7, (every (2ⁱ)^th node has a pointer (2ⁱ) node ahead (i = 1, 2,...); then the number of nodes to be examined can be reduced to $\lceil$ log₂n $\rceil$ while only doubling the number of pointers.

**Figure 3.7:** Every (2ⁱ)^th node has a pointer to a node (2ⁱ)nodes ahead (i = 1, 2,...)
$\begin{figure} \centerline{\psfig{figure=figures/Flist3.ps}} \end{figure}$

**Figure 3.8:** A skip list
$\begin{figure} \centerline{\psfig{figure=figures/Fskiplist1.ps}} \end{figure}$

A node that has k forward pointers is called a level k node. If every (2ⁱ)^th node has a pointer (2ⁱ) nodes ahead, then
# of level 1 nodes 50 %
# of level 2 nodes 25 %
# of level 3 nodes 12.5 %
Such a data structure can be used for fast searching but insertions and deletions will be extremely cumbersome, since levels of nodes will have to change.
What would happen if the levels of nodes were randomly chosen but in the same proportions (Figure 3.8)?
- level of a node is chosen randomly when the node is inserted
- A node's i^th pointer, instead of pointing to a node that is 2^{i - 1} nodes ahead, points to the next node of level i or higher.
- In this case, insertions and deletions will not change the level of any node.
- Some arrangements of levels would give poor execution times but it can be shown that such arrangements are rare.
Such a linked representation is called a skip list.
Each element is represented by a node the level of which is chosen randomly when the node is inserted, without regard for the number of elements in the data structure.
A level i node has i forward pointers, indexed 1 through i. There is no need to store the level of a node in the node.
Maxlevel is the maximum number of levels in a node.
- Level of a list = Maxlevel
- Level of empty list = 1
- Level of header = Maxlevel

3.8.1 Initialization:

Next: 3.8.1 Initialization: Up: 3. Dictionaries Previous: 3.7 Hash Table Restructuring

eEL,CSA_Dept,IISc,Bangalore