


Next: 3.6 Analysis of Closed Hashing
Up: 3.5 Hashing Functions
Previous: 3.5.2 Multiplication Method
This involves choosing a hash function randomly in a way that is
independent of
the keys that are actually going to be stored. We select
the hash function at random from a
carefully designed class of functions.
Example of a universal class of hash functions:
Let table size m be prime. Decompose a key x into r +1 bytes. (i.e.,
characters or fixed-width binary strings). Thus
x = (x0, x1,..., xr)
Assume that the maximum value of a byte to be less than m.
Let
a = (a0, a1,..., ar) denote a sequence of r + 1 elements chosen
randomly from the set
{0, 1,..., m - 1}. Define a hash function
ha 
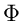 by
by
ha(
x) =
 aixi
aixi mod
m
With this definition,
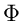 =
=  {ha} can be shown to be universal.
Note that it has mr + 1 members.
{ha} can be shown to be universal.
Note that it has mr + 1 members.



Next: 3.6 Analysis of Closed Hashing
Up: 3.5 Hashing Functions
Previous: 3.5.2 Multiplication Method
eEL,CSA_Dept,IISc,Bangalore
![]()
![]() by
by