Let U = universe of keys
Let the hash values be 0, 1, . . . , m-1
Let us assume that each key is drawn independently from U according
to a probability distribution P. i.e., for k ![]() U
U
P(k) = Probability that k is drawn
Then simple uniform hashing requires that
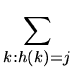 P(k)
=
P(k)
= ![]() for each j = 0, 1,..., m - 1
for each j = 0, 1,..., m - 1
that is, each bucket is equally likely to be occupied.
Suppose the keys are known to be random real numbers k independently and uniformly distributed in the range [0,1).
Qualitative information about P is often useful in the design process. For example, consider a compiler's symbol table in which the keys are arbitrary character strings representing identifiers in a program. It is common for closely related symbols, say pt, pts, ptt, to appear in the same program. A good hash function would minimize the chance that such variants hash to the same slot.
- The division method computes the hash value as the remainder when the key is divided by a prime number. Unless that prime is somehow related to patterns in the distribution P, this method gives good results.