


Next:3.5.3
Universal HashingUp:3.5
Hashing FunctionsPrevious:3.5.1
Division Method
3.5.2 Multiplication Method
There are two steps:
-
1.
-
Multiply the key k by a constant A in the range 0 < A
< 1 and extract the fractional part of kA
-
2.
-
Multiply this fractional part by m and take the floor.
-
h(k)
=
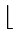 m(kA
mod 1)
m(kA
mod 1)
where
| |
|
kA mod 1 = kA - 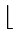 kA kA |
|
| |
|
h(k) = 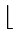 m(kA
- m(kA
- 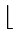 kA kA ) ) |
|
-
Advantage of the method is that the value of m is not critical.
We typically choose it to be a power of 2:
m = 2p



Next:3.5.3
Universal HashingUp:3.5
Hashing FunctionsPrevious:3.5.1
Division Method
eEL,CSA_Dept,IISc,Bangalore
![]() A.2w
A.2w![]() .
The result is a 2w - bit value
.
The result is a 2w - bit value
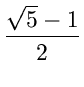 = 0.6180339887... (Golden Ratio)
= 0.6180339887... (Golden Ratio)