9.5 Heap Sort

Worst case as well as average case running time is O(nlog n)

REF.

Robert W. Floyd. Algorithm 245 (TreeSort). Communications of the ACM, Volume 7, pp. 701, 1964.

REF.

J.W.J. Williams. Algorithm 232 (Heapsort). Communications of the ACM, Volume 7, pp. 347-348, 1964.

• Heap: Recall that a heap is a complete binary tree such that the weight of every node is less than the weights of its children.

 

 
 


Figure 9.1: Example of a heap


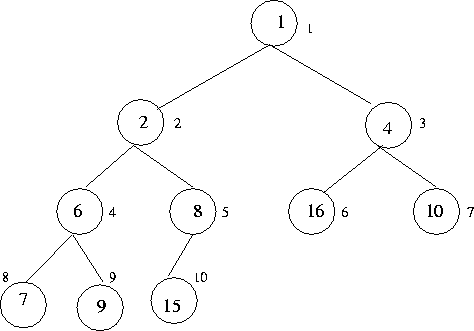• A heap with n elements can be conveniently represented as the first nelements of an array. Furthermore, the children of a[i] can be found in a[2i] (left child) and a[2i + 1] (right child)
• See Figure 9.1 for an example
• Generic heap sort algorithm:

 

 
 
 

    {

            Insert all records to form a heap S;

            while (S is not empty)

                {

                    y = min (S);

                    print the value of y;

                    delete y from S;

                }

    }

Heap sort crucially uses a function called pushdown (first, last).

This assumes that the elements a[first], a[first + 1], ..., a[last] obey the heap property, except possibly the children of a[first]. The function pushes a[first] down until the heap property is restored.

Example: See Figure 9.2. Here, a[1],..., a[10] is a heap except that the children of a[1]violate the heap property.

Figure 9.2: Illustration of some heap operations

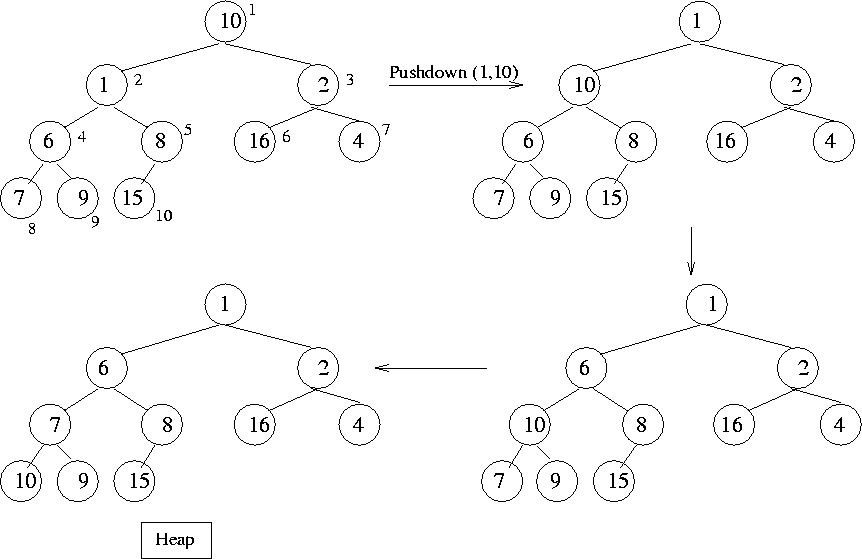Heapsort Algorithm

    {

            for$\left(\vphantom{i = \frac{n}{2}, i >= 1; i--}\right.$i = ${\frac{n}{2}}$, i > = 1;i - -$\left.\vphantom{i = \frac{n}{2}, i >= 1; i--}\right)$

                    pushdown (i, n); /* initial heap construction */

            for(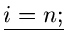$\underline{i = n;}$ i > = 2;i - -)

            {

            swap records a[i] and a[1];

            pushdown (1, i - 1)

            }

    }

• It can be shown that the initial heap construction takes O(n) time in the worst case.
• The sorting portion takes worst case O(nlog n) time.
• Heap sort can also be used for computing order statistics, ie., k^thlowest in a list of records.