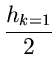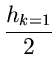Next: 9.5 Heap Sort
Up: 9. Sorting Methods
Previous: 9.3 Selection Sort
- Invented by David Shell. Also called as Diminishing Increments sort.
- REF.
- Shell. A High-speed Sorting Procedure.
Communications of the ACM, Volume 2, Number 7, pp. 30-32,1959.
- The algorithm works by comparing elements that are distant; the
distance between comparisons decreases as the algorithm runs until the
last phase, in which adjacent elements are compared.
- Uses an increment sequence,
h1, h2,..., ht. Any increment
sequence will do as long as h1 = 1, however some choices are better
than others.
- After a phase, using some increment hk, for every i, we have
a[
i]
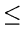 a
a[
i +
hk]
whenever i +
hk 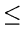 n
n
That is, all elements spaced h apart are sorted and the sequence is
said to be
hk - sorted
- The following shows an array after some phases in shellsort.
| OriginalArray |
81 |
94 |
11 |
96 |
12 |
35 |
17 |
95 |
28 |
58 |
41 |
75 |
15 |
| After5-Sort |
35 |
17 |
11 |
28 |
12 |
41 |
75 |
15 |
96 |
58 |
81 |
94 |
95 |
| After3-Sort |
28 |
12 |
11 |
35 |
15 |
41 |
58 |
17 |
94 |
75 |
81 |
96 |
95 |
| After1-Sort |
11 |
12 |
15 |
17 |
28 |
35 |
41 |
58 |
75 |
81 |
94 |
95 |
96 |
- An important property of Shellsort:
- A sequence which is hk - sorted that is then hk - 1 - sorted
will remain hk - sorted.
This means that work done by early phases is not undone by later phases.
- The action of an hk - sorted is to perform an insertion sort on
hk independent subarrays.
- Shell suggested the increment sequence
For various reasons, this turns out to be a poor choice of increments.
Hibbard suggested a better sequence;
1, 3, 7,...2k - 1.
- Worst-case running time of Shellsort, using shell's increments, has
been shown to be O(n2)
- Worst-case running time of Shellsort, using Hibbard's increments,
has been shown to be
O(n1.5)
- Sedgewick has proposed several increment sequences that give an
O(n
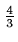 worst-case running time.
worst-case running time.
- Showing the average -case complexity of shellsort has proved to be a
formidable theoretical challenge.
- Far more details, refer [weiss94, chapter 7, 256-260] and [knuth 73].



Next: 9.5 Heap Sort
Up: 9. Sorting Methods
Previous: 9.3 Selection Sort
eEL,CSA_Dept,IISc,Bangalore
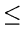 a[i + hk] whenever i + hk
a[i + hk] whenever i + hk 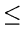 n
n
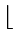
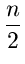
 ;hk =
;hk =