8.4.2 Optimal Solution for TSP using Branch and Bound

Principle

Suppose it is required to minimize an objective function. Suppose that we have a method for getting a lower bound on the cost of any solution among those in the set of solutions represented by some subset. If the best solution found so far costs less than the lower bound for this subset, we need not explore this subset at all.

Let S be some subset of solutions. Let

  L(S) = a lower bound on the cost of

$$\mbox{any solution belonging to $S$ }$$

Let  C = cost of the best solution found so far

If C$\leq$L(S),	there is no need to explore S because it does
	not contain any better solution.
If C > L(S),	then we need to explore S because it may
	contain a better solution.

A Lower Bound for a TSP

Note that:

Cost of any tour

                = $${\textstyle\frac{1}{2}}$$$$\sum_{v \in V}^{}$$$$\begin{array}{l} \mbox{(Sum of the costs ofthe two tour } \\ \mbox{ edges adjacent to $v$)}\end{array}$$
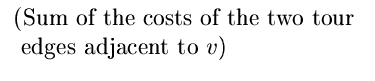
Now:

The sum of the two tour edges adjacent to a given vertex v

                $$\geq$$   sum of the two edges of least cost adjacent to  v

Therefore:
 

Cost of any tour
 
                $$\geq$$$${\textstyle\frac{1}{2}}$$$$\sum_{v \in V}^{}$$$$\begin{array}{l} \mbox{(Sum of thecosts of the two least cost } \\ \mbox{edges adjacent to $v$)}\end{array}$$
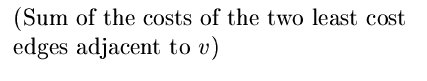
Example: See Figure 8.17.
 
 

Figure 8.17: Example of a complete graph with five vertices

 

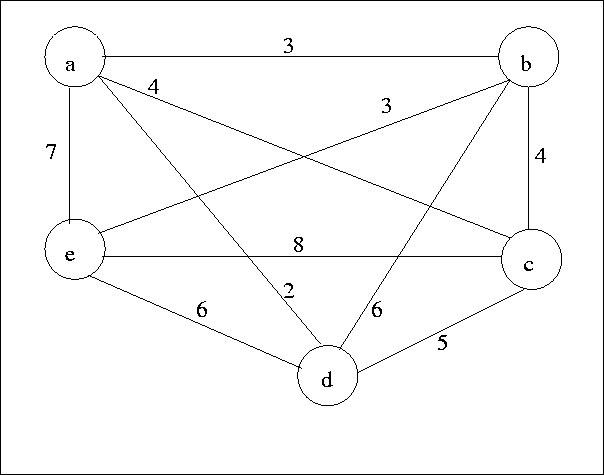Node	Least cost edges	Total cost
a	(a, d), (a, b)	5
b	(a, b), (b, e)	6
c	(c, b), (c, a)	8
d	(d, a), (d, c)	7
e	(e, b), (e, f)	9

Thus a lower bound on the cost of any tour = $${\textstyle\frac{1}{2}}$$ (5 + 6 + 8 + 7 + 9) = 17.5 A solution Tree for a TSP instance: (edges are considered in lexicographic order): See Figure 8.18
 
 

Figure 8.18: A solution tree for a TSP instance

• Suppose we want a lower bound on the cost of a subset of tours defined by some node in the search tree.


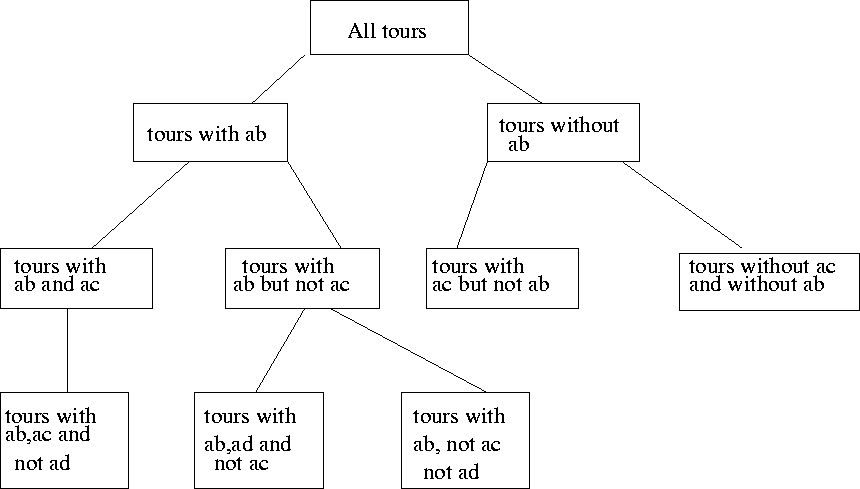In the above solution tree, each node represents tours defined by a set of edges that must be in the tour and a set of edges that may not be in the tour.

• These constraints alter our choices for the two lowest cost edges at each node.


e.g., if we are constrained to include edge (a, e), and exclude (b, c), then we will have to select the two lowest cost edges as follows:

a	(a, d), (a, e)	9
b	(a, b), (b, e)	6
c	(a, c), (c, d)	9
d	(a, d), (c, d)	7
e	(a, e), (b, e)	10

Therefore lower bound with the above constraints = 20.5

• Each time we branch, by considering the two children of a node, we try to infer additional decisions regarding which edges must be included or excluded from tours represented by those nodes. The rules we use for these inferences are:

1.

If excluding (x, y) would make it impossible for x or y to have as many as two adjacent edges in the tour, then (x, y) must be included.

2.

If including (x, y) would cause x or y to have more than two edges adjacent in the tour, or would complete a non-tour cycle with edges already included, then (x, y) must be excluded.

• See Figure 8.19.
• When we branch, after making what inferences we can, we compute lower bounds for both children. If the lower bound for a child is as high or higher than the lowest cost found so far, we can ``prune'' that child and need not consider or construct its descendants.


Interestingly, there are situations where the lower bound for a node n is lower than the best solution so far, yet both children of n can be pruned because their lower bounds exceed the cost of the best solution so far.

• If neither child can be pruned, we shall, as a heuristic, consider first the child with the smaller lower bound. After considering one child, we must consider again whether its sibling can be pruned, since a new best solution may have been found.

Figure 8.19: Branch and bound applied to a TSP instance