


Next:8.4.2
Optimal Solution for TSP using Branch and BoundUp:8.4
Traveling Salesman ProblemPrevious:8.4
Traveling Salesman Problem
8.4.1 A Greedy Algorithm for
TSP
-
Based on Kruskal's algorithm. It only gives a suboptimal solution in general.
-
Works for complete graphs. May not work for a graph that is not complete.
-
As in Kruskal's algorithm, first sort the edges in the increasing order
of weights.
-
Starting with the least cost edge, look at the edges one by one and select
an edge only if the edge, together with already selected edges,
-
1.
-
does not cause a vertex to have degree three or more
-
2.
-
does not form a cycle, unless the number of selected edges equals the number
of vertices in the graph.
Example:
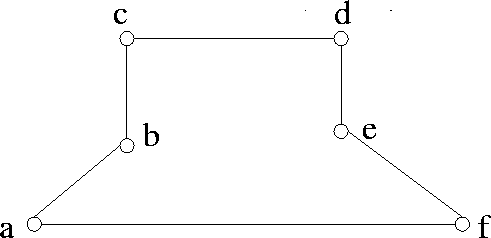
Consider the six city problem shown in Figure 8.14.
The sorted set of edges is
{ (d,
e),
3
(d,
e),
3 ,
, (b,
c),
5
(b,
c),
5 ,
, (a,
b),
5
(a,
b),
5 ,
, (e,
f
), 5
(e,
f
), 5 ,
,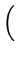 (a,
c),
7.08
(a,
c),
7.08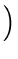 ,
,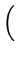 (d,
f
),
(d,
f
),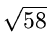
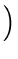 ,
,
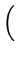 (b,
e),
(b,
e),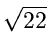
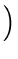 ,
,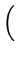 (b,
d
),
(b,
d
),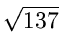
 ,
, (c,
d
), 14
(c,
d
), 14 ,...
,... (a,
f
), 18
(a,
f
), 18
See Figures 8.15 and 8.16.
Figure 8.15: An intermediate stage in the construction
of a TSP tour
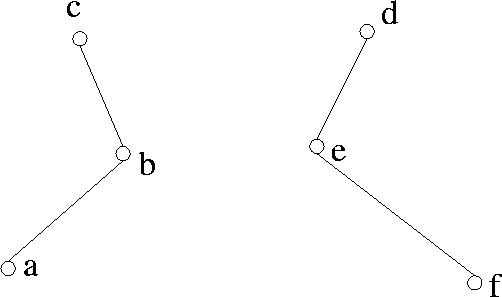 |
Select (d, e) |
|
| Select (a, b) |
|
| Select (b, c) |
|
| Select (e, f) |
|
| Reject (a, c) |
since it forms a cycle with (a, b) and (b, c) |
| Reject (d, f) |
since it forms a cycle with (d, e) and (e, f) |
| Reject (b, e) |
since that would make the degree of b equal to 3 |
| Reject (b, d) |
for an identical reason |
| Select (c, d) |
|
| . |
|
| . |
|
| . |
|
| Select (a, f) |
|
| |
|
This yields a total cost = 50, which is about 4% from the optimal cost. |
|
Figure 8.16: A TSP tour for the six-city problem
 |



Next:8.4.2
Optimal Solution for TSP using Branch and BoundUp:8.4
Traveling Salesman ProblemPrevious:8.4
Traveling Salesman Problem
eEL,CSA_Dept,IISc,Bangalore
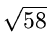
![]() (d,
e),
3
(d,
e),
3![]() ,
,![]() (b,
c),
5
(b,
c),
5![]() ,
,![]() (a,
b),
5
(a,
b),
5![]() ,
,![]() (e,
f
), 5
(e,
f
), 5![]() ,
,![]() (a,
c),
7.08
(a,
c),
7.08![]() ,
,![]() (d,
f
),
(d,
f
),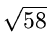
![]() ,
,
![]() (b,
e),
(b,
e),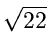
![]() ,
,![]() (b,
d
),
(b,
d
),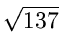
![]() ,
,![]() (c,
d
), 14
(c,
d
), 14![]() ,...
,...![]() (a,
f
), 18
(a,
f
), 18![]()

