    The generalized vickery auction(GVA) is a generalized single round second price sealed bid auction, wherein the payment made by the winner(winners) of the auction is determined by the second highest bid.
    The method used to determine the payment made by the winner(winners) is
as follows:
    a)For every winner of the auction,we derive his marginal contribution to the auction i.e. the difference between the revenue to the market in the presence of his bids and the revenue that would have been generated if his bids were absent.
    b)The payment made by a winner is his bid amount minus his marginal contribution to the auction as determined by (a).

Properties of GVA:

a) The GVA is allocatively efficient.
b) The GVA is truth revealing i.e. it encourages the bidders to place
the bid close to the their true valuation of the product.

How does GVA achieve truth revealation:

The mechanism of the GVA business model is designed in such a way that bidders
receive maximum profit when they place bids equal to their true valuation of the
product. Lets see how.
Suppose X is the allocation vector for the bids placed X:
X = {x1,x2,x3,.........xn} where xi = 1 if bid number i is present in the allocation,
                                              = 0, otherwise.
G = {1,2,3.........m} is the set of goods/items.
I = {a1,a2,a3.......am} is the set of agents.
J = {b1,b2,b3....bN} is the set of bids.
W = {w1,w2,w3......wN}is the bid vector,
                    where wj is the bid price of jth bid.
A=[aij] { m*n matrix}
                    aij=1 if item i is in the bid j.
                    aij=0 otherwise
We want to maximize the vector product WX subjected to following constraints:
The vector product AX<=1 (an item should belong to only one bid allocated)
There are two phases of GVA:
1) Allocation phase :Determine X*(optimal bid allocation vector)
2) Determine the payments made by the winner(winners).
Let C be a winning bidder.
X(c)* is that part of X* which belongs to the bids from C.
X(-c)* is the remaining part of X* i.e.optimal allocation bid vector when C is not bidding.Bids of C have not been included in X(-c)*.
Now we maximize W(-c)X(-c) subject to A(-c)X(-c)<=1
Let Z(-c)* be the optimal solution to the above equation
Hence Revenue to the market without C will be W(-c)Z(-c)*.
Vickery Discount for C (as determined by GVA rule)
will be equal to WX* - W(-c)Z(-c)*.
Payment by C = Amount C has bid-His discount.
Now the amount C has bid will be equal to the summation of product of all of his bids
with the corresponding bid prices.i.e. W(c)X(c)*.
Hence payment by C = W(c)X(c)*-(WX* - W(-c)Z(-c)* ).
Now we are going to show that GVA ensures truth revealation by maximizing the profit
of bidder if he reveals(bids) the true value for the product.
Revenue of C for arbitrary bid prices(not necessarily equal to the true valuation)
will be the difference between the value of C for items allocated and the actual payment made by him.
Suppose V is the true valuation vector for C.
Revenue= V(c)X(c)*-W(c)X(c)*+WX* - W(-c)Z(-c)*.
Revenue=V(c)X(c)*+W(-c)X(-c)* - W(-c)Z(-c)*...............(1)
Now suppose bidder C bids his true value of the product
Our job now is to maximize V(c)X(c)+W(-c)X(-c)
Let XT be the optimal solution of the above.
Now revenue of the bidder C when he reveals his true value
equals V(c)XT(c)+W(-c)XT(-c)-W(-c)Z(-c)* ...............(2)
The differences between (1) and (2) are:
(a) V(c)XT(c) - V(c)X(c)* which is nonnegative and
(b) W(-c)XT(-c) - W(-c)X(-c)* which is nonpositive.
Now (a) indicates that when bidder C has revealed his true value
his revenue is definitely increased(or remains the same) because in the allocation
vector X there will be more bids which are allocated to C hence (a) will always be nonnegative quantity.
On the other hand (b) will always be a nonpositive quantity because whenC bids
true value there will be less elements in XT(-c) * which are 1 than in X(-c) *.
So the net result of (a) and (b) decides whether C has gained something or not.
We now show that the net difference is greater in (a) than in (b).
Since revealation of true value by C certainly helps him winning more or equal bids than before,these extra wins can only occur if the elements in V(c) which caused these wins are greater than corresponding elements(for the same bid) of W(-c) which really is the case.
Hence it is proved that C's revenue will be maximum when he bids his true value.

Sandholm Algorithm:

The winner determination can be done by dynamic programming but that takes O(3^m) where m = |G|. By putting certain restrictions on the bidding process winner determination can be done in polynomial time. But that makes the bidding process extremely restrictive.

Sandholm algorithm is used for efficiently finding optimal allocation . The motivations behind Sandholm algorithm are :

    1. allow all possible combination of bids.
    2. given enough time find the optimal (not approximate) solution.
    3. capitalize heavily on the sparseness of bids. This is in contrast with the dynamic algorithm which takes the same time irrespective of the number of bids.

Sandholm algorithm can also allow an auctioneer to 'keep' an item. 'Keep'ing an item means it is not allocated to any bidder. It can be proved that the option of keeping an item may increase the revenue of the auctioneer in case there are no bids of positive value on that item alone.
The option of keeping can be incorporated as a preprocessing step where dummy bids of zero value are added for those individual items which have received no bids alone.

Sandholm algorithm works by constructing an allocation tree such that every relevant partition is represented by one and only one path from the root to a leaf.

   The algorithm is as follows:
         a) Every product is given an index starting from 1 upto the total number
             of products.
         b) The allocation tree is constructed from the root in the following way:
                i. include the item with the lowest index among the items that has not yet been included in the current path yet,
                ii. do not include items that has already been included in the path.

This process is repeated for all the products until all the paths of the tree contain all the products (including dummy bids). It means every path from a root to leaf of the tree will represent one of the partitions of the set of all products.

Now the optimal allocation will comprise of all the nodes of "optimal path" of the allocation tree. By optimal path we mean the path for which the sum of the bid values is optimal (maximum or minimum depending on the requirements of optimality). In fact if it is a procurement problem we can also use pruning to further make algorithm more efficient.

Sandholm algorithm can be extended to provide for X-OR bidding. In X-OR bidding the bidder can bid on a number of combinations such that at most one of them is allocated. This can be implemented by including a dummy item in each of the X-OR bids.

Example:

Now we are going to show one example of how GVA determines the winner(s) and
the payment made by them using Sandholm algorithm for winner determination.
Suppose there are 5 products (A,B,C,D,E) to be sold and 3 buyers,name them x,y,z.
The bids placed by the three bidders x,y,z are as follows:
                x: (A,30) ,(B,20) ,(BC,30),(C,5),(CDE,30).
                y: (ABC,45),(CD,30),(D,10),(E,5).
                z: (A,10),(BC,40),(C,10),(DE,30).
We are not assuming any XOR constraint here ,that means it is possible
that more than one bid of a buyer get selected in the optimal bid allocation vector.
Just looking at the bid combination we easily come to know that following bids
can not be selected(because higher bids are available for the same bundle).
                (z,A.10) ,(x,BC,30) ,(x,C,5)
Applying the Sandholm algorithm,we obtain the following allocation tree.

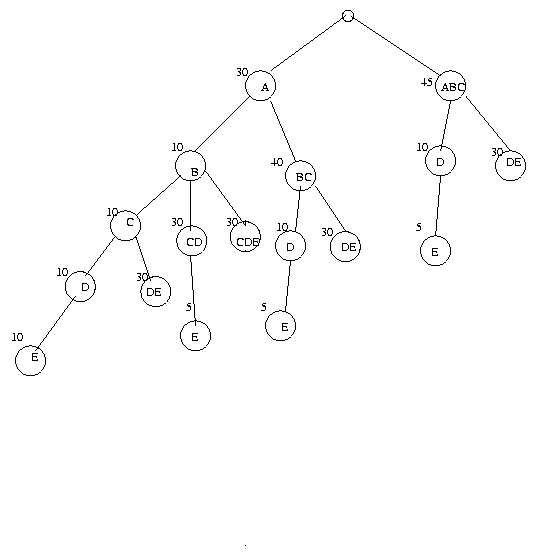
                            ALLOCATION TREE FOR THE GIVEN EXAMPLE

From the above tree we find that the maximum revenue to the seller will occur
if the following bids are selected:
                (x,A,30),(z,BC,40),(z,DE,30).
The optimal allocation vector is: X*=(1000000000101)
The revenue to the seller(market) is 30+40+30=100.
Now comes the issue of the payment made by the winners x and z.
The payment made by x:
                  For this we remove x from the bidding scenario and now obtain the
                  optimal allocation of the bids .
                 We find that in absence of x the bids which are selected:
                 (z,A,10),(z,BC,40),(z,DE,30).
                 The revenue to the market is 10+40+30=80.
                 The marginal contribution of x to the market is 100-80=20.
                 Hence the payment made by x is 30-20=10.
The payment made by z:
                 Now we remove z from the bidding scene, the optimal allocation
                 of bids include the following bids:
                 (x,A,30),(x,B,20),(y,CD,30)(y,E,5).
                  The revenue to the market is 30+20+30+5=85.
                  The marginal contribution of z to the market is 100-85=15.
                  Hence the payment made by z= (40+30)-15,that is 55.
In this way the payments made by x and z are 10 and 55 respectively
instead of their original bids of 30 and (30+40=70) .

Disadvantages of GVA:

Following are the disadvantages of GVA:
1)Winner determination problem is NP-hard.
2) Upto m (number of products) payment determination problems are to be solved which are again NP-hard.

Bibliography:

1. Achieving Budget-Balance with Vickrey - Based Payment Schemes in Exchanges - David C. Parkes and Jayant Kalagnanam and Marta Eso

2. Generalized Vickrey auctions - J. rey and K. MacKie-Mason and H. Varian

3. An Iterative Generalized Vickrey Auction: Strategy-Proofness without Complete revealation - David C. Parkes

4. Truth Revelation in Rapid, Approximately Efficient Combinatorial Auctions - Daniel Lehmann,Liadan Ita O'Callaghan

5. Algorithm for optimal winner determination in Combinatorial Auctions - Tuomas Sandholm