An E-Procurement system provides the automation of negotiations between buyers and sellers using reverse auction. It is a market place where there is one buyer and multiple sellers.
A Configurable offer is made by the seller in response to the RFQ provided by the buyer. Configurable offers allow multiple values for each attribute and they include rules on how to combine the various attribute values and how to price a desired configuration. A Configurable offer consists of collection of configurations where each configuration specifies a selection for each of the many attributes of the component. From a configurable offer, a user can extract offers for individual configurations.
Consider PCs. PC vendors describe their offerings along number of attributes on their Web site, and each of these attributes can take multiple values. This way, customers can configure and order a PC tailored to their individual needs. For example, suppose a PC has only three attributes, namely processor speed, hard disk size, operating system, and price. A supplier could specify that there are three processors available {850MHz, 950 MHz, and 1GHz}, as well as two sizes of hard disks {10GB and 15GB}. The base configuration (850MHz, 10GB) prices for $1000. A configuration with a 1GHz computer is $100 more, and one with a 15GB hard disk costs an additional $200. Of course, there can be many more rules, which need to be considered. For example, a certain operating system might require a minimal processor speed to function properly, and the supplier might specify a linear decreasing volume discount.
where Vj is the set of allowable values for attribute j. This allows for a very large number of configurations based on the size of Vj. The two issues regarding representation are :
TOP
- representing the price for each allowable configuration, and
- representing configuration constraints and price promotions.
This model forces the suppliers to provide a functional description of price as a function of the attributes. Assuming the additive price function where the impact of each attribute on price is additive, this model formalizes the mark up based pricing schemes where a price mark up is associated with each level of an attribute. The price mark-up for each attribute can be non linear as shown below. Assuming additivity of the attributes, the total price pi for a particular bid/offer i can be written as:
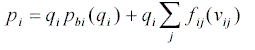
where qi is quantity, pbi(qi) is the base price per item as a function of quantity (i.e. specifies a volume discount), and fij(vij) is a functional specification for the impact of particular attribute values vij on the price of a product. The individual functions pbi(qi) and fji(vij) can in general be nonlinear. For any attribute j, the difference fji(vij,=vj,hi) fji(vij = vj,base) represents the price markup for level hi with respect to the base level.
In addition a configurable offer can specify so called add on rules (TAG: AddOnRules). Add on rules have the form of a logical equivalence or an implication with an antecedent and a conclusion. The antecedent can be any logical proposition including conjunctions, disjunctions, negations as well as atomic propositions. The conclusion defines in addition a Markup tag, which specifies a certain discount or markup. This way, suppliers can specify a certain discount as a result of the selected attribute values.
A configurable offer is one of a sequence of messages and a response to a particular request, which specifies a buyer's basic requirements. The tags defined in CPML can be used standalone or they can also be embedded to enrich existing catalogue standards.
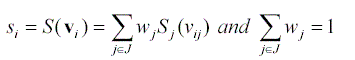
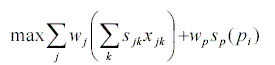
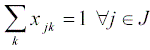
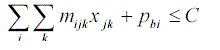
For getting the top L solutions, the following
constraints are added.
Let us denote the Lth optimal solution by a set
of indices NL that indicate the levels chosen for each attribute. For example
for the optimal solution this set is N1 and we can eliminate the optimal
solution from our search by adding the constraint where | N 1| is the cardinality
of the set.
For 2nd best solution add the following constraint:
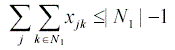

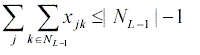
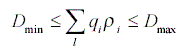
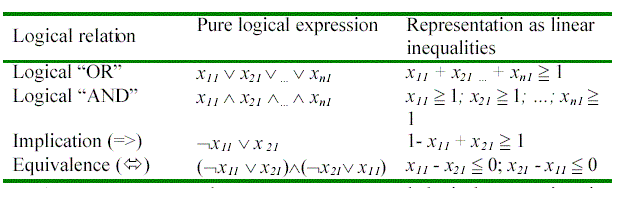

| C | unit reservation price |
| Dmin | lower bound for a buyer's demand |
| Dmax | upper bound for a buyer's demand |
| fij(vij) | defines the price markup for a particular attribute value vij of offer I |
| I | set of offers |
| J | set of attributes |
| Kj | set of attribute values for attribute j |
| L | set of configurations |
| mijk | markup of level k of attribute j |
| NL | set of indices for the Lth best solution |
| Omin | maximum number of winning suppliers |
| Omax | maximum number of winning suppliers |
| pbi(qi) | price of a base configuration for an offer as a function of quantity |
| pi | total price for a particular offer i |
| p- | a discount or markup specified in logical propositions about configuration rules |
| qi | total quantity for a particular offer i |
| si | score of offer i |
| Sj(.) | scoring function for attribute j |
| S(vi) | set of attribute values for attribute j |
| sp(pi) | linear (decreasing) scoring function on price |
| Tjk | set of all bids at level K for attribute J |
| Vj | set of allowable values for attribute j |
| vij | value of attribute j of offer i |
| wj | weight of attribute j |
| xijk | a binary indicator variable for a particular attribute level vij |
| yi | an indicator variable that one particular offer has been chosen |
| zjk | indicator variable that assumes the value 1 if any suppliers are chosen with a bid at level k for attribute j |
| ri | best configuration from offer i based on a given scoring function |