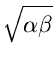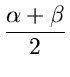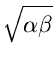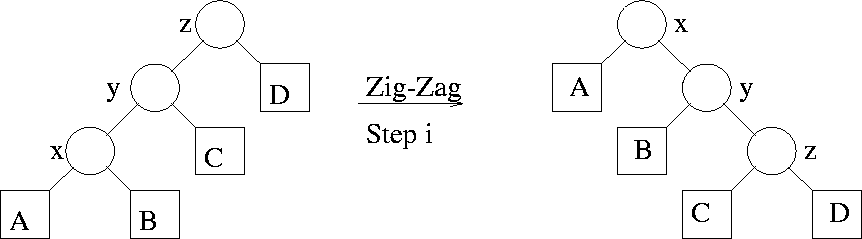Next: 4. Binary Trees
Up: 4.6 Amortized Algorithm Analysis
Previous: 4.6.4 Example of Incrementing Binary Integers
- As a measure of complexity, we shall take the depth within the tree that
the desired node has before splaying.
| T |
: |
BST on which we are performing a splay |
| |
|
insertion or retrieval |
| |
|
|
| Ti |
: |
tree T as it has been transformed after |
| |
|
step i of the splaying process, with T0 = T |
| |
|
|
| x |
: |
any node in Ti |
| Ti(x) |
: |
subtree of Ti with root x |
| | Ti(x)| |
: |
number of nodes of Ti(x) |
- We consider bottom-up splaying at a node x, so that x begins
somewhere in the tree T but after m splaying steps, ends up as the root of
T.
- Rank
For each step i of the splaying process and each vertex x 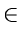 T, we define
rank at step i of x to be
T, we define
rank at step i of x to be
ri(
x) =
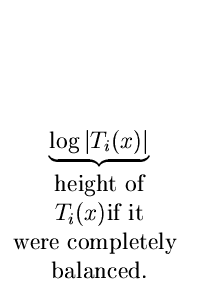
- Portion out the credit balance of the tree among all its vertices by
requiring the following credit invariant to hold:
For every node x of T and after every step i of splaying, node x has
credit equal to its rank ri(x).
- Define the total credit balance for the tree as
Ci =
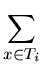 ri
ri(
x)
- If the tree is empty or contains only one node, then its credit balance
is 0. As the tree grows, its credit balance increases. The credit balance
should reflect the work needed to build the tree.
- Our goal is to determine bounds on ai that will allow us to find the
cost of the splaying process, amortized over a sequence of retrievals and
insertions.
- A useful Result:
If
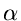 ,
,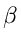 ,
,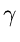 are positive real numbers with
are positive real numbers with
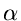 +
+ 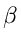
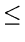
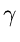 , then
, then
This can be easily proved as follows:
| |
|
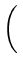 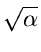 -
- 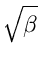
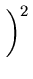
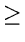 0
0 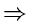
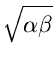
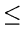
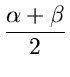
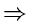
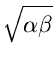
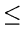
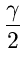 |
(4.22) |
| |
|
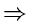 log
log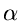 + log
+ log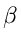
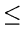 2log
2log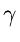 - 2
- 2 |
|
Result 1
If the ith splaying step is a zig-zig or a zag-zag step at node
x, then its amortized complexity ai satisfies
ai < 3(ri(x) - ri - 1(x))
See Figure 4.26.
Figure 4.26:
A zig-zig at the ith splaying step
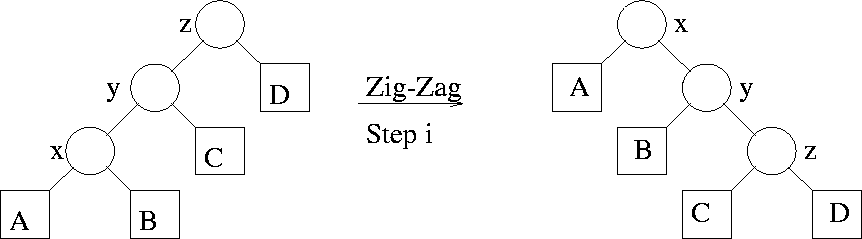 |
- The actual complexity ti of a zig-zig or a zag-zag is 2 units
- Only the sizes of the subtrees rooted at x, y, z change in this
step. Hence, all terms in the summation defining Ci cancel against those
for Ci - 1 except those indicated below
| ai |
= |
ti + Ci - Ci - 1 |
(4.23) |
| |
= |
2 + ri(x) + ri(y) + ri(z) |
(4.24) |
| |
|
- ri - 1(x) - ri - 1(y) + ri - 1(z) |
(4.25) |
| |
= |
2 + ri(y) + ri(z) - ri - 1(x) - ri - 1(y) (  )
) |
|
Since
| Ti(x)| = | Ti - 1(z)| as the subtree
rooted at z before the
splaying step has the same size as that rooted at x after the step.
Let
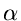 = | Ti - 1(x)|,
= | Ti - 1(x)|,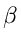 = | Ti(z)|, and
= | Ti(z)|, and
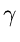 = | Ti(x)|. Then observe
that
= | Ti(x)|. Then observe
that
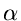 +
+ 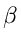
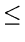
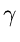 . This is because
. This is because
| Ti - 1(x) contains components x, A, B |
|
|
(4.26) |
| Ti(z) contains components z, C, D |
|
|
(4.27) |
Ti(x) 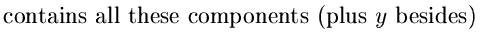 . . |
|
|
|
Thus by (*)
ri - 1(
x) +
ri(
z)
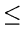
2
ri(
x) - 2
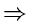
2
ri(
x) -
ri - 1(
x) -
ri(
z) - 2
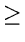
0
Adding this to ( ), we get
), we get
ai 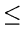
2
ri(
x) - 2
ri - 1(
x) +
ri(
y) -
ri - 1(
y)
Before step i, y is the parent of x so that
| Ti - 1(y)| > | Ti - 1(x)|
After step i, x is the parent of y so that
| Ti(x)| > | Ti(y)|
Taking logarithms we have
ri - 1(y) > ri - 1(x) and ri(x) > ri(y)
Thus we obtain
ai < 3ri(x) - 3ri - 1(x)
Similarly, we can show Results 2 and 3 below:



Next: 4. Binary Trees
Up: 4.6 Amortized Algorithm Analysis
Previous: 4.6.4 Example of Incrementing Binary Integers
eEL,CSA_Dept,IISc,Bangalore
![]() T, we define
rank at step i of x to be
T, we define
rank at step i of x to be
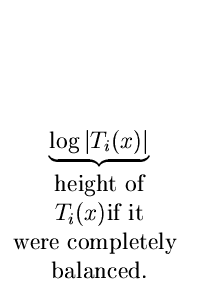
![]() ,
,![]() ,
,![]() are positive real numbers with
are positive real numbers with
![]() +
+ ![]()
![]()
![]() , then
, then