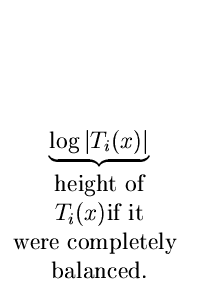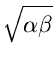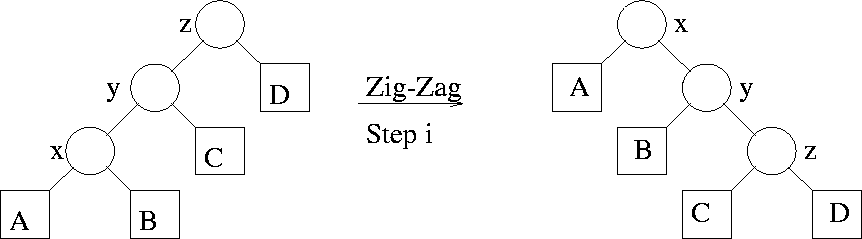Next:4.7
To Probe FurtherUp:4.6
Amortized Algorithm AnalysisPrevious:4.6.4
Example of Incrementing Binary Integers
4.6.5 Amortized Analysis of Splaying
-
As a measure of complexity, we shall take the depth within the tree that
the desired node has before splaying.
| T |
: |
BST on which we are performing a splay |
| |
|
insertion or retrieval |
| |
|
|
| Ti |
: |
tree T as it has been transformed after |
| |
|
step i of the splaying process, with T0
= T |
| |
|
|
| x |
: |
any node in Ti |
| Ti(x) |
: |
subtree of Ti with root x |
| | Ti(x)| |
: |
number of nodes of Ti(x) |
-
We consider bottom-up splaying at a node x, so that x begins
somewhere in the tree T but after m splaying steps, ends
up as the root of
T.
-
Rank
For each step i of the splaying process and each vertex x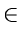 T,
we define rank at step i of x to be
T,
we define rank at step i of x to be
ri(x) = 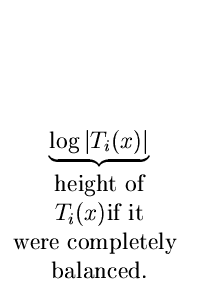
-
Portion out the credit balance of the tree among all its vertices by requiring
the following credit invariant to hold:
For every node x of T and after every step i of
splaying, node x has credit equal to its rank ri(x).
-
Define the total credit balance for the tree as
Ci = 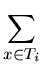 ri(x)
Result 1
ri(x)
Result 1
If the ith splaying step is a zig-zig or a zag-zag
step at node
x, then its amortized complexity ai
satisfies
ai < 3(ri(x) - ri
- 1(x))
See Figure 4.26.
Figure 4.26: A zig-zig at the ith splaying step
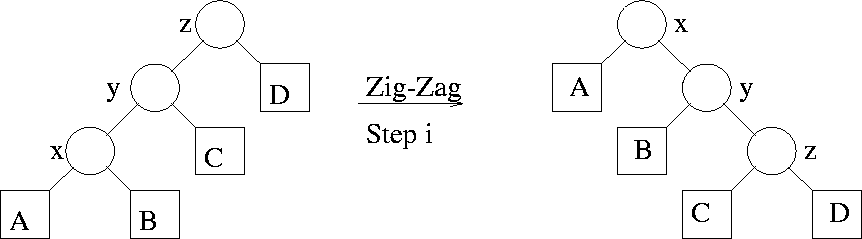 |
-
The actual complexity ti of a zig-zig or a zag-zag is
2 units
-
Only the sizes of the subtrees rooted at x, y, z change
in this step. Hence, all terms in the summation defining Ci
cancel against those for Ci - 1 except those indicated
below
| ai |
= |
ti + Ci - Ci
- 1 |
|
| |
= |
2 + ri(x) + ri(y)
+ ri(z) |
|
| |
|
- ri - 1(x)
- ri - 1(y) + ri - 1(z) |
|
| |
= |
2 + ri(y) + ri(z)
- ri - 1(x) - ri - 1(y)
(  )
) |
|
Since | Ti(x)|
= | Ti - 1(z)| as the subtree rooted at z
before the splaying step has the same size as that rooted at x after
the step.
Let
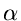 = | Ti - 1(x)|,
= | Ti - 1(x)|,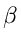 = | Ti(z)|, and
= | Ti(z)|, and 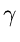 = | Ti(x)|. Then observe that
= | Ti(x)|. Then observe that 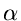 +
+ 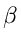
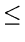
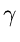 .
This is because
.
This is because
|
Ti - 1(x) contains components x,
A, B |
|
|
|
| Ti(z) contains components
z, C, D |
|
|
|
Ti(x) 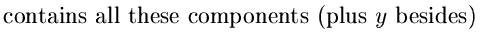 . . |
|
|
|
Thus by (*)
ri - 1(x) + ri(z) 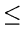 2ri(x) - 2
2ri(x) - 2
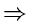 2ri(x) - ri - 1(x) -
ri(z)
- 2
2ri(x) - ri - 1(x) -
ri(z)
- 2 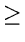 0
Adding this to (
0
Adding this to ( ),
we get
ai
),
we get
ai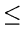 2ri(x) - 2ri - 1(x) +
ri(y)
- ri - 1(y)
Before step i, y is the parent of x so that
| Ti - 1(y)| > | Ti - 1(x)|
After step i, x is the parent of y so that
| Ti(x)| > | Ti(y)|
Taking logarithms we have
ri - 1(y) > ri - 1(x)
and ri(x) > ri(y)
Thus we obtain
ai < 3ri(x) - 3ri
- 1(x)
Similarly, we can show Results 2 and 3 below:
2ri(x) - 2ri - 1(x) +
ri(y)
- ri - 1(y)
Before step i, y is the parent of x so that
| Ti - 1(y)| > | Ti - 1(x)|
After step i, x is the parent of y so that
| Ti(x)| > | Ti(y)|
Taking logarithms we have
ri - 1(y) > ri - 1(x)
and ri(x) > ri(y)
Thus we obtain
ai < 3ri(x) - 3ri
- 1(x)
Similarly, we can show Results 2 and 3 below:
Result 2
If the ith splaying step is a zig-zag or zag-zig at node x, then its amortized
complexity ai satisfies
ai < 2(ri(x) - ri
- 1(x))
Result 3
If the ith splaying step is a zig or a zag, then
ai < 1 + (ri(x) -
ri
- 1(x))
Result 4
The total amortized cost over all the splaying steps can be computed
by adding the costs of all the splay steps. If there are k such steps,
only the last can be a zig or zag and the others are all zig-zag or
zig-zag or zag-zig or zag-zag. Since (*) provides the weaker bound,
we get,
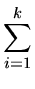 ai ai |
= |
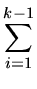 ai
+ ak ai
+ ak |
|
| |
|
|
|
| |
 |
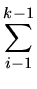 3(ri(x) - ri - 1(x))
+ (1 + 3rk(x) - 3rk - 1(x))
3(ri(x) - ri - 1(x))
+ (1 + 3rk(x) - 3rk - 1(x)) |
|
| |
|
|
|
| |
= |
1 + 3rk(x) - 3r0(x) |
|
| |
|
|
|
| |
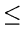 |
1 + 3rk(x) |
|
| |
|
|
|
| |
= |
1 + 3log n |
|
Thus the amortized cost of an insertion or retrieval with splaying in
a BST with n nodes does not exceed 1
+ 3log n upward moves of the target node in the tree.
Result 5
Now consider a long sequence of m splay insertions or retrievals. We
seek to compute the actual cost of all these m operations.
Let Tj and Aj be the actual cost and amortized cost of the jthoperation,
where j = 1, 2,...,
m, now represents
a typical insertion or retrieval operation.
We have
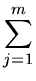 Tj
=
Tj
= 
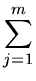 Aj
Aj +
+  If the tree never has more than n nodes, then C0 and Cm lie between 0 and
log n, so that
If the tree never has more than n nodes, then C0 and Cm lie between 0 and
log n, so that
C0 - Cm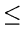 log n
log n
Also we know that
Aj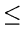 1 + 3logn for j = 1, 2,..., m
1 + 3logn for j = 1, 2,..., m
Thus the above becomes
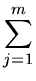 Tj
= m(1 + 3logn) + log n
Tj
= m(1 + 3logn) + log n
The above gives the total actual time of m insertions or retrievals
on a tree that never has more than n nodes.
This gives O(log n) actual running time for each operation.



Next:4.7
To Probe FurtherUp:4.6
Amortized Algorithm AnalysisPrevious:4.6.4
Example of Incrementing Binary Integers
eEL,CSA_Dept,IISc,Bangalore
![]() T,
we define rank at step i of x to be
T,
we define rank at step i of x to be