3.3.1 Open Hashing

Let:

• U be the universe of keys:
  • integers
  • character strings
  • complex bit patterns
• B the set of hash values (also called the buckets or bins). Let B = {0, 1,..., m - 1}where m > 0 is a positive integer.

A hash function h : U $\rightarrow$ B associates buckets (hash values) to keys.

Two main issues:

1.

Collisions

If x₁ and x₂ are two different keys, it is possible that h(x₁) = h(x₂). This is called a collision. Collision resolution is the most important issue in hash table implementations.

2.

Hash Functions

Choosing a hash function that minimizes the number of collisions and also hashes uniformly is another critical issue.

Collision Resolution by Chaining

• Put all the elements that hash to the same value in a linked list. See Figure 3.1.

  

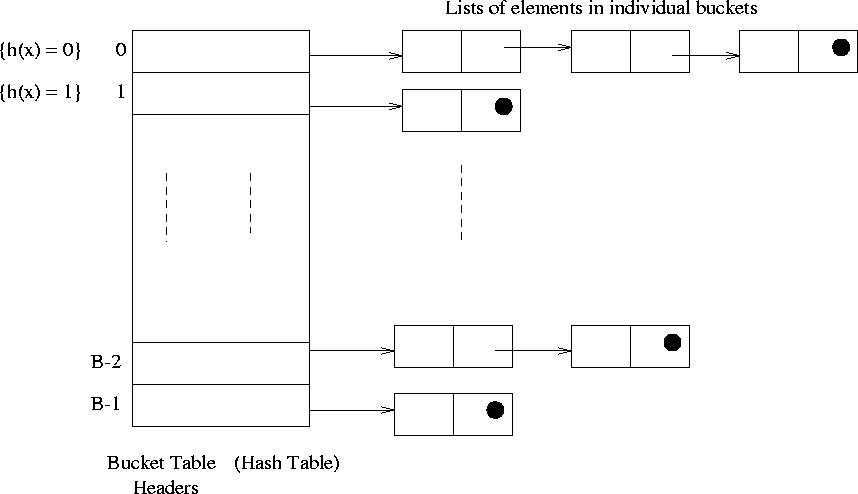
Figure 3.1: Collision resolution by chaining

Example:

See Figure 3.2. Consider the keys 0, 1, 4, 9, 16, 25, 36, 49, 64, 81, 100. Let the hash function be:

h(x) = x % 7

  

Figure 3.2: Open hashing: An example

• Bucket lists
  • unsorted lists
  • sorted lists (these are better)

• Insert (x, T)

  Insert x at the head of list T[h(key (x))]

• Search (x, T)

  Search for an element x in the list T[h(key (x))]

• Delete (x, T)

  Delete x from the list T[h(key (x))]

Worst case complexity of all these operations is O(n)

In the average case, the running time is O(1 + $\alpha$), where

$$\alpha \;\stackrel{\Delta}{=}\; {\frac{n}{m}}$$ = (3.1)

n =  number of elements stored (3.2)

m =  number of hash values or buckets

It is assumed that the hash value h(k) can be computed in O(1) time. If n is O(m), the average case complexity of these operations becomes O(1) !