


Next:9.11
To Probe FurtherUp:9.
Sorting MethodsPrevious:9.9
Radix Sorting
9.10 Merge Sort
-
Divide and conquer algorithm
-
O(nlog n) worst case performance
-
Useful in external sorting applications.
Algorithm
list-type mergesort (list-type L; int
n)
{
if (n = 1)
return (L)
else {
split L into two halves L1and
L2;
return (merge (mergesort 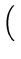 L1,
L1,
 ,
mergesort
,
mergesort 
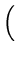 L2,
L2,
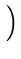

}
}
Let T(n) be the running time of mergesort
on a list of size n. Then.
| T(n) |
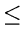 |
C1 (n = 1) |
|
| |
|
|
|
| |
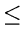 |
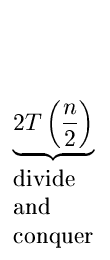 +
+  (n > 1)
(n > 1) |
|
It can be shown that T(n) is O(nlog
n).
Mergesort as an External Sorting Procedure
-
Assume that the data to be sorted is stored in a file
-
The essential idea is to organize a file into progressively larger
runs
where:
A run is a sequence of records r1,...,
rk,
such that ri ri
+ 1 for i = 1,...,
k
- 1.
ri
+ 1 for i = 1,...,
k
- 1.
-
We say a file, r1,
r2,...,
rm,
of records is organized into
runs or length
k if:
 i
i  1 such that ki
1 such that ki  m,
the sequence
m,
the sequence
 rk(i
- 1) + 1, rk(i - 1) + 2,..., rki
rk(i
- 1) + 1, rk(i - 1) + 2,..., rki is a run of length k and furthermore if m is not divisible
by k and m = pk +
q
where q < k, the sequence (rm
- q + 1,..., rm) which is called the tail
is a run of length q.
is a run of length k and furthermore if m is not divisible
by k and m = pk +
q
where q < k, the sequence (rm
- q + 1,..., rm) which is called the tail
is a run of length q.
Example
The following is organized into runs of length 3 with the tail having
length 2.
| 7 15 29 |
8 11 13 |
16 22 31 |
5 12 |
Basic step
Consider two files f1 and f2 organized into runs of length k. Assume
that
-
1.
-
If ni is the number of runs (including tails) of f1(i
= 1, 2), then | n1
- n2|
 1
1
-
2.
-
At most one of f1 and f2 has a tail
-
3.
-
The one with a tail (if any) has at least as many runs as the other.
In mergesort, we read one run from each of f1
and f2, merge the runs into a run of
length 2k and append it to one of two files g1
and g2. By alternating between g1
and g2, these files would be organized into runs
of length 2k, satisfying (1), (2), and (3).
Algorithm
-
First divide all n records into two files f1 and
f2
as evenly as possible. f1 and f2 can
be regarded as organized into runs of length 1.
-
Merge the runs of length 1 and distribute them into files g1
and g2which will now be organized into runs of length
2.
-
Now make f1 and f2 empty and merge
g1
and g2 into f1 and
f2
creating runs of length 4.
Repeat ...
Example
| f1 |
28 |
3 |
93 |
54 |
65 |
30 |
90 |
10 |
69 |
8 |
22 |
| f2 |
31 |
5 |
96 |
85 |
9 |
39 |
13 |
8 |
77 |
10 |
|
runs of length 1
 merge into
g1 and g2
merge into
g1 and g2
| g1 |
28 |
31 |
93 |
96 |
9 |
65 |
13 |
90 |
69 |
77 |
22 |
| g2 |
3 |
5 |
54 |
85 |
30 |
39 |
8 |
10 |
8 |
10 |
|
runs of length 2
 merge into
f1 and f2
merge into
f1 and f2
| f1 |
3 |
5 |
28 |
31 |
9 |
30 |
39 |
65 |
8 |
10 |
69 |
77 |
| f2 |
54 |
85 |
93 |
96 |
8 |
10 |
13 |
90 |
22 |
|
|
|
runs of length 4
 merge into
g1 and g2
merge into
g1 and g2
| g1 |
3 |
5 |
28 |
31 |
54 |
85 |
93 |
96 |
8 |
10 |
22 |
69 |
77 |
| g2 |
8 |
9 |
10 |
13 |
30 |
39 |
65 |
90 |
|
|
|
|
|
runs of length 8
 merge
into
f1 and f2
merge
into
f1 and f2
| f1 |
3 |
5 |
8 |
9 |
10 |
13 |
28 |
30 |
31 |
| |
39 |
54 |
65 |
85 |
90 |
93 |
96 |
|
|
| |
|
|
|
|
|
|
|
|
|
| f2 |
8 |
10 |
22 |
69 |
77 |
|
|
|
|
runs of length 16
 merge into
g1 and g2
merge into
g1 and g2
g1 will be left with the sorted sequence
Multiway Mergesort
-
Here we merge m files at a time. Let the files f1,...,
fm
be organized as runs of length k.
We can read m runs, one from each file, and merge them into one
run of length
mk. This run is placed on one of m files g1,...,
gm,
each getting a run in turn.
-
The merging process will involve each time selecting the minimum among
m
currently smallest unselected records from each file.
By using a priority queue that supports insert and delete in logarithmic
time (e.g., partially ordered tree), the process can be accomplished in
O(log
m)time.
-
Number of passes -
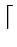 logmn
logmn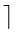
Effort in each pass = O(nlog2m)
overall complexity 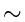 O(nlog2m.logmn)
O(nlog2m.logmn)
-
Advantages
-

-
We save by a factor of log2m, the number of times we
read each record
-

-
We can process data O(m) times faster with m disk
units.



Next:9.11
To Probe FurtherUp:9.
Sorting MethodsPrevious:9.9
Radix Sorting
eEL,CSA_Dept,IISc,Bangalore
![]() L1,
L1,![]()
![]() ,
mergesort
,
mergesort ![]()
![]() L2,
L2,![]()
![]()
![]()
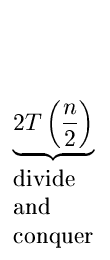 +
+  (n > 1)
(n > 1)![]() ri
+ 1 for i = 1,...,
k
- 1.
ri
+ 1 for i = 1,...,
k
- 1.
![]() merge into
g1 and g2
merge into
g1 and g2
![]() merge into
f1 and f2
merge into
f1 and f2
![]() merge into
g1 and g2
merge into
g1 and g2
![]() merge
into
f1 and f2
merge
into
f1 and f2
![]() merge into
g1 and g2
merge into
g1 and g2
![]() logn
logn![]()
![]()
![]()
![]() O
O![]()
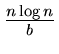
![]() .
.