Note that the presence of equal keys will make the sorting easier, not harder.
Let T(n) = average time taken by quicksort to sort n elements
The left group can have i elements where i = 1, 2,..., n - 1, since the left group has at least one element and the right group also has at least one element.
Let us fix i and try to compute the probability:
P{ left group has i elements}
Now, left group has i elements
![]() pivot
must be the (i + 1)stelement
among the n elements
pivot
must be the (i + 1)stelement
among the n elements
If the pivot is in position 1, then the element in position 2 is one of the i smaller elements and vice-versa.
P{ Position 1 contains one of the i smaller elements }
= ![]()
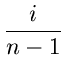
![]()
![]()
![]()
![]()
Similarly,
P{ Position 2 contains one of the i smaller elements}
= ![]()
![]()
![]()
![]()
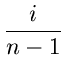
![]()
Therefore,
P{ left group has i elements}
= 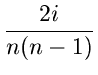
This leads to
T(n) ![]() C2n
+
C2n
+ ![]()
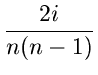
![]() T(i)
+ T(n - i)
T(i)
+ T(n - i)![]()
Using
![]() f
(i) =
f
(i) = ![]() f
(n - i),
f
(n - i),
we get
T(n) ![]() C2n
+
C2n
+ 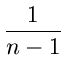
![]()
![]() T(i)
+ T(n - i)
T(i)
+ T(n - i)![]()
The above expression is in the form it would have been if we had picked
a truly random pivot at each step.
The above simplifies to:
T(n) ![]() C2n
+
C2n
+ 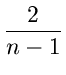
![]() T(i)
T(i)
The above is the recurrence that one would get if all sizes between
1 and n - 1for the left group were equally likely. Thus picking the larger
of the two elements doesn't really affect the size distribution.
We shall guess the solution
T(n) ![]() Cnlog
n
Cnlog
n
for some constant C and prove its correctness
using induction.
Basis:
n = 2 ![]() Cnlog
n
= 2C
Cnlog
n
= 2C
which is correct.
Induction Step:
AssumeT(i) ![]() Cilogi
Cilogi![]() i
< n.
i
< n.
| T(n) | C2n + 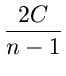 |
||
C2n + 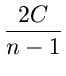 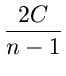  ilog
i ilog
i |
|||
C2n + 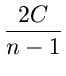 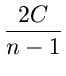  ilog
n ilog
n |
|||
C2n + Cnlogn
- 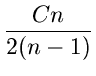 ,simplification ,simplification |
PickingC![]() 4C2, we have,
4C2, we have,
C2n - ![]()
![]() 0
0
Thus T(n) is O(nlog
n)