


Next:7.6
To Probe FurtherUp:7.5
Directed Acyclic GraphsPrevious:7.5.2
Topological Sort
7.5.3 Strong Components
-
REF.
-
Rao S. Kosaraju. Unpublished. 1978.
-
REF.
-
Robert E. Tarjan. Depth first search and linear graph algorithms.
SIAM
Journal on Computing, Volume 1, Number 2, pp. 146-160, 1972.
-
A strongly connected component of a digraph is a maximal set of vertices
in which there is a path from any one vertex to any other vertex in the
set. For an example, see Figure 7.15.
Figure 7.15: Strong components of a digraph
 |
-
Let G = (V, E) be a digraph. We can partition V
into equivalence classes Vi,
1
 i
i  r,
such that vertices v and w are equivalent if there is a path
from v to w and a path from w to v.
r,
such that vertices v and w are equivalent if there is a path
from v to w and a path from w to v.
Let Ei,
1  i
i r,
be the set of arcs with head and tail both in
Vi.
r,
be the set of arcs with head and tail both in
Vi.
Then the graphs (Vi,
Ei) are called the strong components of G.
A digraph with only one strong component is said to be strongly connected.
-
Depth-first-search can be used to efficiently determine the strong components
of a digraph.
-
Kosaraju's (1978) algorithm for finding strong components in a graph:
-
1.
-
Perform a DFS of G and number the vertices in order of completion of the
recursive calls.
-
2.
-
Construct a new directed graph Gr by reversing the direction
of every arc in G.
-
3.
-
Perform a DFS on Gr starting the search from the highest
numbered vertex according to the numbering assigned at step 1. If the DFS
does not reach all vertices, start the next DFS from the highest numbered
remaining vertex.
-
4.
-
Each tree in the resulting spanning forest is a strong component of
G.
Figure 7.16: Step 1 in the strong components algorithm
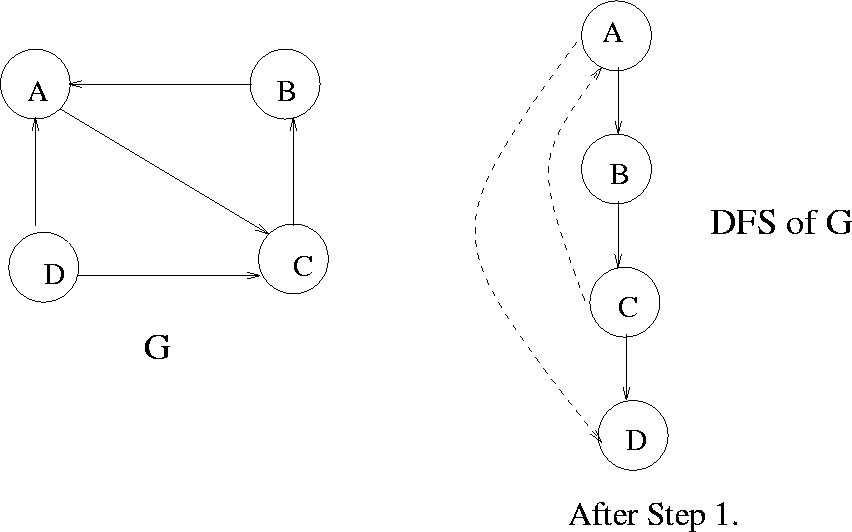 |
Figure 7.17: Step 3 in the strong components algorithm
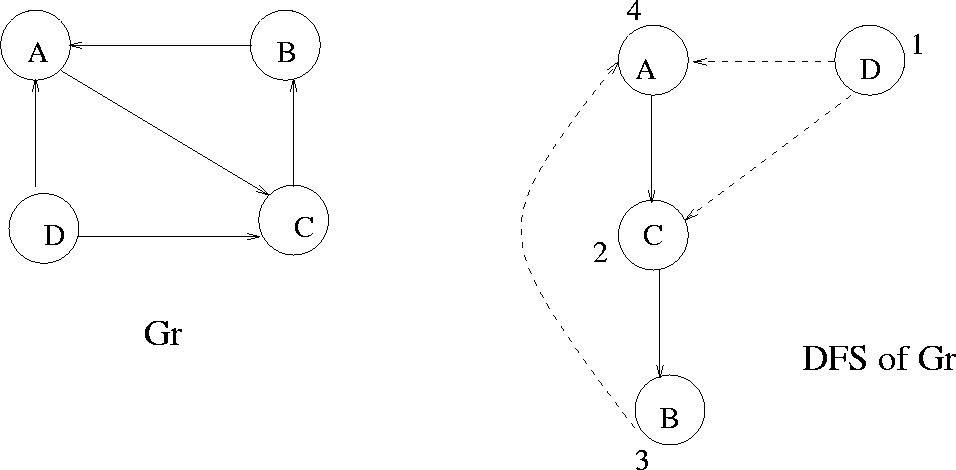 |
Example: See Figures 7.16
and 7.17
Proof of Kosaraju's Algorithm
| |
u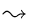 x x |
|
(7.16) |
| |
+ |
|
|
| |
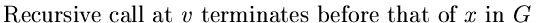 |
|
(7.17) |
In the DFS of G, there are
two possibilities.
| 1) |
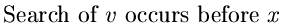 |
|
(7.18) |
| 2) |
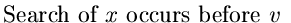 |
|
(7.19) |
| (1),(3) |
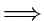 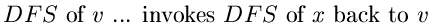 . . |
| |
  . . |
| |
 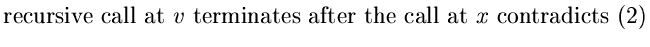 . . |
| |
|
| |
 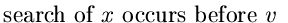 . . |
| (4),(2) |
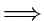 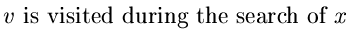 . . |
| |
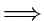 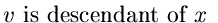 . . |
| |
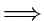  . . |
| |
  . . |
| |
|
| |
Similarly,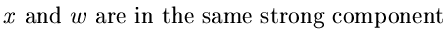 . . |
| |
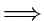 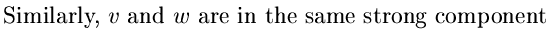 . . |



Next:7.6
To Probe FurtherUp:7.5
Directed Acyclic GraphsPrevious:7.5.2
Topological Sort
eEL,CSA_Dept,IISc,Bangalore

![]() i
i![]() r,
be the set of arcs with head and tail both in
Vi.
r,
be the set of arcs with head and tail both in
Vi.

