


Next: 7.4.1 Breadth First Search
Up: 7. Directed Graphs
Previous: 7.3 Warshall's Algorithm
- An important way of traversing all vertices of a digraph, with
applications in many problems.
- Let L[v] be the adjacency list for vertex v. To do a depth first
search of all vertices emanating from v, we have the following recursive
scheme:
void dfs (vertex v)
{
vertex w;
mark v as visited;
for each vertex w 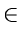 L[v]
L[v]
dfs(w)
}
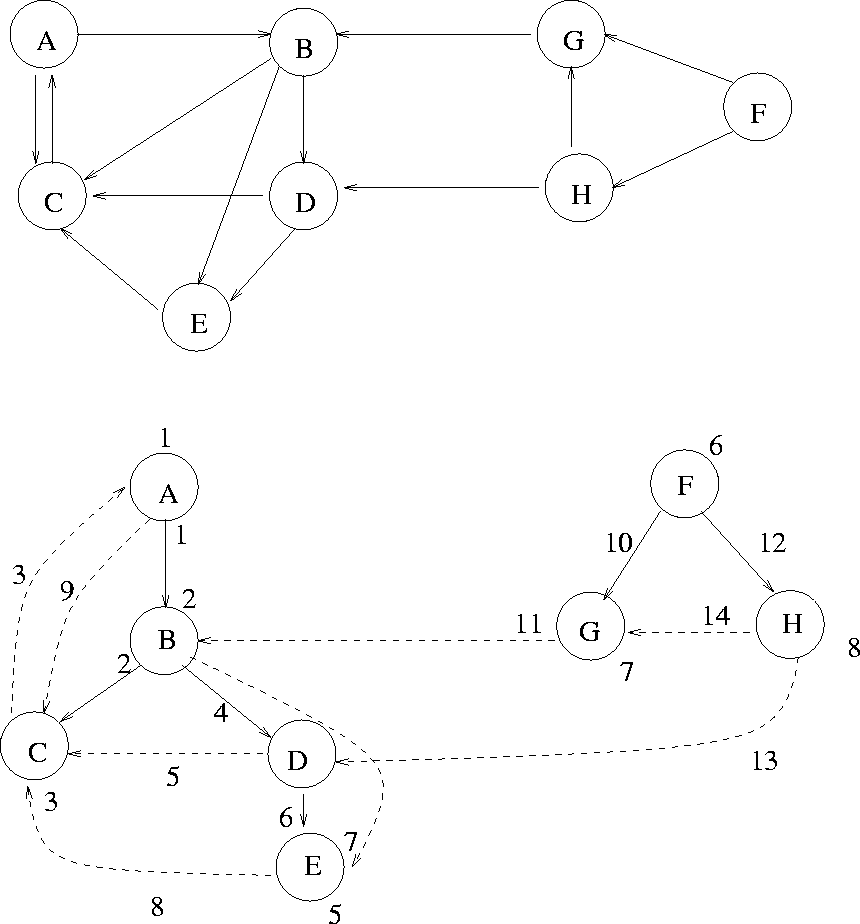
Figure 7.10:
Depth first search of a digraph
 |
- To do a dfs on the entire digraph, we first unmark all vertices and
do a dfs on all unmarked vertices:
{
for v 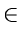 V
V
mark v as unvisited;
for v 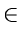 V
V
if (v is unvisited)
dfs(v);
}
Example: See Figure 7.10.
DFS Arcs:
- Tree Arcs:
a
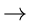 b, N(a) < N(b) leading to unvisited
vertices
b, N(a) < N(b) leading to unvisited
vertices
- Non-Tree Arcs:
- back
arcs:
a
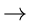 b, N(a)
b, N(a) 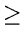 N(b), b is an ancestor
N(b), b is an ancestor
-
forward arcs:
a
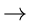 b, N(a) < N(b), b is a proper
descendant
b, N(a) < N(b), b is a proper
descendant
- cross arcs:
a
 b. Neither ancestor nor
descendant
b. Neither ancestor nor
descendant



Next: 7.4.1 Breadth First Search
Up: 7. Directed Graphs
Previous: 7.3 Warshall's Algorithm
eEL,CSA_Dept,IISc,Bangalore
![]() L[v]
L[v]
![]() V
V
![]() V
V
![]() L[v]
L[v]
![]() V
V
![]() V
V