7.1 Directed Graphs

A directed graph or digraph G comprises

1. a set of vertices V

2. a set of directed edges or arcs, E (an arc is an ordered pair of vertices)

Example: See Figure 7.1
 
 

Figure 7.1: A digraph with 4 vertices and 5 arcs

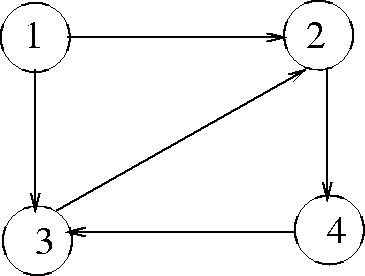V = {1, 2, 3, 4}

E = {(1,2), (1,3), (2,4), (3,2), (4,3)}

• If there is an arc (v, w), we say w is adjacent to v.
• A path is a sequence of vertices v₁, v₂,...v_n such that the vertex pairs (v₁, v₂),(v₂, v₃), ..., (v_{n - 1}, v_n) are arcs in the graph. The length of a path is the number of arcs on the path. A single vertex v by itself denotes a path of length zero.
• A path v₁, v₂,..., v_n is said to be simple if the vertices are distinct, except possibly v₁ and v_n. If v₁ = v_n and n > 1, we call such a path a simple cycle.