


Next:4.9.3
Comparison of Skip Lists and Splay TreesUp:4.9
Programming AssignmentsPrevious:4.9.1
Huffman Coding
4.9.2 Comparison of Hash Tables
and Binary Search Trees
The objective of this assignment is to compare the performance of open
hash tables, closed hash tables, and binary search trees in implementing
search, insert, and delete operations in dynamic sets. You can initially
implement using C but the intent is to use C++ and object-oriented principles.
Generation of Keys
Assume that your keys are character strings of length 10 obtained by
scanning a text file. Call these as tokens. Define a token as any string
that appears between successive occurrences of a forbidden character, where
the forbidden set of characters is given by:
F = {comma, period, space}
If a string has less than 10 characters, make it up into a string of
exactly 10 characters by including an appropriate number of trailing *'s.
On the other hand, if the current string has more than 10 characters, truncate
it to have the first ten characters only.
From the individual character strings (from now on called as tokens),
generate a positive integer (from now on called as keys) by summing up
the ASCII values of the characters in the particular token. Use this integer
key in the hashing functions. However, remember that the original token
is a character string and this is the one to be stored in the data structure.
Methods to be Evaluated
The following four schemes are to be evaluated.
-
1.
-
Open hashing with multiplication method for hashing and unsorted lists
for chaining
-
2.
-
Open hashing with multiplication method for hashing and sorted lists for
chaining
-
3.
-
Closed hashing with linear probing
-
4.
-
Binary search trees
Hashing Functions
For the sake of uniformity, use the following hashing functions only.
In the following, m is the hash table size (that is, the
possible hash values are, 0,
1,..., m - 1), and x is an integer key.
-
1.
-
Multiplication Method
-
-
h(x) = Floor(m*Fraction(k*x))
where k = 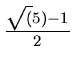 ,
the Golden Ratio.
,
the Golden Ratio.
-
2.
-
Linear Probing
-
-
h(x,
i) = (h(x, 0) + i)
mod
m;i = 0,..., m - 1
Inputs to the Program
The possible inputs to the program are:
-
m: Hash table size. Several values could be given here and the experiments
are to be repeated for all values specified. This input has no significance
for binary search trees.
-
n: The initial number of insertions of distinct strings to be made
for setting up a data structure.
-
M: This is a subset of the set {1,
2, 3, 4} indicating the set of methods to be investigated.
-
I: This is a decimal number from which a ternary string is to be
generated (namely the radix-3 representation of I). In this representation,
assume that a 0 represents the search operation, a 1
represents the insert operation, and a 2 represents the delete
operation.
-
A text file, from which the tokens are to be picked up for setting up and
experimenting with the data structure
What should the Program Do?
-
1.
-
For each element of M and for each value of m, do the following.
-
2.
-
Scan the given text file and as you scan, insert the first n distinct
strings scanned into an initially empty data structure.
-
3.
-
Now scan the rest of the text file token by token, searching for it or
inserting it or deleting it, as dictated by the radix-3 representation
of I. Note that the most significant digit is to be considered first
while doing this and you proceed from left to right in the radix-3 representation.
For each individual operation, keep track of the number of probes.
-
4.
-
Compute the average number of probes for a typical successful search, unsuccessful
search, insert, and delete.



Next:4.9.3
Comparison of Skip Lists and Splay TreesUp:4.9
Programming AssignmentsPrevious:4.9.1
Huffman Coding
eEL,CSA_Dept,IISc,Bangalore
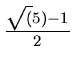 ,
the Golden Ratio.
,
the Golden Ratio.
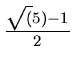 ,
the Golden Ratio.
,
the Golden Ratio.