


Next: 4.8.3 Splay Trees
Up: 4.8 Problems
Previous: 4.8.1 General Trees
- 1.
- Suppose that we have numbers between 1 and 1000 in a binary search
tree and want to search for the number 363. Which of the following
sequences could not be the sequence of nodes examined?
- (a)
- 2, 252, 401, 398, 330, 344, 397, 363.
- (b)
- 924, 220, 911, 244, 898, 258, 362, 363.
- (c)
- 925, 202, 911, 240, 912, 245, 363.
- (d)
- 2, 399, 387, 219, 266, 382, 381, 278, 363.
- (e)
- 935, 278, 347, 621, 299, 392, 358, 363.
- 2.
- In a binary search tree, given a key x, define
successor(x) as the
key which is the successor of x in the sorted order determined by an
inorder tree walk. Define
predecessor(x) similarly. Explain how, given x,
its successor and predecessor may be found.
- 3.
- A binary search tree is constructed by inserting the key values
1, 2, 3, 4, 5, 6, 7 in some order specified by a permutation of
1, ..., 7, into an initially empty tree. Which of these permutations
will lead to a complete binary search tree ( 1 node at level 1, 2 nodes at
level 2, and 4 nodes at level 3)?
- 4.
- Suppose that the search for key k in a binary search tree ends up in
a leaf. Consider three sets: A, the keys to the left of the search path;
B, the keys on the search path; and C, the keys to the right of the search
path. Investigate if the following is true:
a
 b
b  c
c 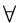 a
a  A; b
A; b  B; c
B; c  C. Give a proof or a
counter-example as the case may be.
C. Give a proof or a
counter-example as the case may be.
- 5.
- Is the operation of deletion in a binary search tree
commutative in
the sense that deleting x and then y from a binary search tree leaves
the same tree as deleting y and then x? Argue why it is so or give a
counter-example.
- 6.
- Devise an algorithm that takes two values, a and b such that
a
 b, and visits all keys x in a BST such that
a
b, and visits all keys x in a BST such that
a  x
x  b.
The running time of your algorithm should be
O(N + log n), where Nis the number of keys visited and n is the number of keys in the tree.
b.
The running time of your algorithm should be
O(N + log n), where Nis the number of keys visited and n is the number of keys in the tree.
- 7.
- A random binary search tree having n nodes, where n = 2k - 1, for
some positive integer k, is to be reorganized into a perfectly balanced
binary search tree. Outline an efficient algorithm for this task. The
algorithm should not use any memory locations other than those already
used by the random binary search tree.
- 8.
- Consider three keys,
k1, k2, k3, such that
k1 < k2 < k3.
A binary search tree is constructed with these three keys. Depending
on the order in which the keys are inserted, five different binary
search trees are possible.
- (a)
- Write down the five binary search trees.
- (b)
- Let p, q, r be the probabilities of probing for
k1, k2, k3, respectively in the given binary search
trees (p + q + r = 1). Compute the average number of comparisons
(or probes) on a successful search for each of the above
five binary search trees.
- (c)
- Define the optimum binary search tree as the one for
which the average number of comparisons on a successful
search is minimum.
Determine the range of values of p, q, r, for which the
completely balanced search tree is the optimum search tree.
- 9.
- Given a set of 31 names, each containing 10 uppercase alphabets,
we wish to set up a data structure that would lead to efficient
average case performance of successful and unsuccessful searches
on this set. It is known that not more than 5 names start
with the same alphabet. Also, assume that successful and unsuccessful
searches are equally likely and that in the event of a successful
search, it is equally likely that any of the 31 names was
searched for. The two likely choices for the data structure are:
- A closed hash table with 130 locations where each location
can accommodate one name.
- A full binary search tree of height 4, where each of the 31
nodes contains a name and lexicographic ordering is used to
set up the BST.
Answer the following questions:
- (a)
- What is the hashing function you would use for the
closed hash table?
- (b)
- Assume that the computation of the hash function
above takes the same time as comparing two given
names. Now, compute the average case running time of
a search operation using the hash table. Ignore
the time for setting up the hash table.
- (c)
- Compute the average case running time of a search
operation using the BST. Ignore the time for setting up the BST.



Next: 4.8.3 Splay Trees
Up: 4.8 Problems
Previous: 4.8.1 General Trees
eEL,CSA_Dept,IISc,Bangalore