4.8.1 General Trees

1.

Show in any binary tree that the number of leaves is one more than the number of nodes of degree two.

2.

The degree of a node in a tree is the number of children the node has. If a tree has n₁ nodes of degree 1, n₂ nodes of degree 2, ..., n_m nodes of degree m, compute the number of leaves in the tree in terms of n₁, n₂,..., n_m.

3.

Show that if T is a k-ary tree with n nodes, each having a fixed size, then nk + 1 - n of the nk link fields are null links (n 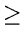$\geq$ 1).

4.

Provide an efficient O(n) time algorithm to determine the height of a tree containing n nodes, represented using parent links. You may build any other supporting data structures, if needed.

5.

Associate a weight w(x) = 2^-d with each leaf x of depth d in a binary tree T. Show that

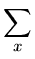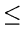
$$\sum_{x}$$w(x) $$\leq$$ 1

where the sum is taken over all leaves x in T.

6.

Consider a complete binary tree with an odd number of nodes. Let n be the number of internal nodes (non-leaves) in the tree. Define the internal path length, I, as the sum, taken over all the internal nodes of the tree, of the depth of each node. Likewise, define the external pathlength, E, as the sum, taken over all the leaves of the tree, of the depth of each leaf. Show that E = I + 2n.

7.

What is the optimal Huffman code for the following set of frequencies, based on the first 8 Fibonacci numbers?

a	b	c	d	e	f	g	h
1	1	2	3	5	8	13	21

Write down the resulting Huffman tree. Can you generalize your answer to find the optimal code when the frequencies are the first n Fibonacci numbers?