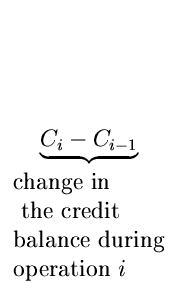4.6.3 Credit Balance

• The credit function behaves like the bank balance of a well-budgeted family. It will be large when the next operation is expensive and smaller when the next operation can be done quickly.
• Consider a sequence of m operations on a data structure. Let 

                                                                                                        t_i = Actual cost of operation i for    1 $$\leq$$i$$\leq$$m

Let the values of the credit between balance function be 

                                                                             C₀, C₁, C₂,..., C_m

C₀ = Credit balance before the first operation

C_i = Credit balance after operation  i


 

Amortized Cost

• The amortized cost a_i of each operation i is defined by 

                                                a_i = t_i + $$\underbrace{C_i - C_{i-1}}_{\begin{array}{l}\mbox{change in} \\......the credit} \\\mbox{balance during}\\\mbox{operation $i$} \end{array}}^{}\,$$

 

choose the credit balance function C_i so as to make the amortized costs a_i as nearly equal as possible, no matter how the actual costs may vary.

We have

t_i = a_i - C_i + C_{i - 1}

$$\sum_{i=1}^{m}$$ = (a₁ - C₁ + C₀) + (a₂ - C₂ + C₁) + ^... + (a_m - C_m + C_{m - 1})

$$\left(\vphantom{\sum_{i=1}^m \space a_i}\right. \sum_{i=1}^{m} \left.\vphantom{\sum_{i=1}^m \space a_i}\right)$$ =

Thus 

$$\sum_{i=1}^{m}$$t_i = $$\left(\vphantom{\sum_{i=1}^m \space a_i}\right.$$$$\sum_{i=1}^{m}$$a_{i$$\left.\vphantom{\sum_{i=1}^m \space a_i}\right)$$} + C₀ - C_m
• Thus the total actual cost can be computed in terms of the amortized costs and the initial and final values of the credit balance function.